题目内容
6．
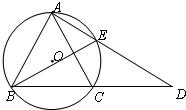如图，⊙O是△ABC的外接圆，AB=AC，延长BC到点D，使得CD=AC，连结AD交⊙O于点E，连结BE，若∠D=35°，则∠ABE的大小为35°．
分析 利用等腰三角形的性质、圆的同弧所对的圆周角相等性质即可得出．
解答 解：∵AC=CD，∠D=35°，
∴∠CAD=35°，∠ACB=70°．
∴∠CBE=35°．
∵AB=AC，
∴∠ABC=70°，
∴∠ABE=35°．
故答案为：35°．
点评 本题考查了等腰三角形的性质、圆的同弧所对的圆周角相等性质，属于基础题．
练习册系列答案
相关题目
16．已知正项数列{an}满足（n+1）an+12-nan2+an+1an=0，且a1=1，不等式“a1•a2+a2•a3+…+an•an+1≥m对任意n∈N*恒成立，则实数m的取值范围是（ ）
| A． | （-∞，$\frac{1}{2}$] | B． | （-∞，$\frac{1}{2}$） | C． | （-∞，1] | D． | （-∞，1） |
17．已知棱长为$\sqrt{2}$四面体ABCD的各顶点在同一个球面上，则该球的体积为（ ）
| A． | $\frac{1}{3}$π | B． | $\frac{2}{3}$π | C． | $\frac{\sqrt{3}}{2}$π | D． | 3π |
16．已知sinα-cosα=$\frac{1}{2}$，且α∈（0，π），则sinα+cosα=（ ）
| A． | $\frac{{\sqrt{7}}}{2}$ | B． | $-\frac{{\sqrt{7}}}{2}$ | C． | $±\frac{{\sqrt{7}}}{2}$ | D． | $±\frac{1}{2}$ |