题目内容
15.已知集合A={x|x2-x-12≤0},B={x|2m-1<x<m+1}(1)若m=-1,求A∩∁RB;
(2)若A∪B=A,求实数m的取值范围.
分析 (1)若m=-1,化简集合,即可求A∩∁RB;
(2)若A∪B=A,B⊆A,利用集合关系即可求实数m的取值范围.
解答 解:(1)若m=-1,则B={x|-3<x<0},
所以CRB={x|x≤-3或x≥0},(2分)
又A={x|(x-4)(x+3)≤0}={x|-3≤x≤4},(4分)
所以A∩CRB={x|0≤x≤4或x=-3};(5分)
(2)因为A∪B=A所以B⊆A,(6分)
当B=Φ时,显然B⊆A,
此时2m-1≥m+1解得m≥2;(8分)
当B≠Φ时,则由B⊆A得-3≤2m-1<m+1≤4,
解得-1≤m<2;(11分)
综合上述,实数m的取值范围为m≥-1.(12分)
点评 本题主要考查集合的基本运算,根据集合关系建立不等式关系是解决本题的关键.

练习册系列答案
相关题目
5.函数y=7tan(-$\frac{1}{2}$x+$\frac{π}{3}$)的最小正周期是( )
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
7.复数z满足(z+2)(1+i3)=2(i为虚数单位),则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
4.设i为虚数单位,则复数$\frac{5-i}{1+i}$的共轭复数为( )
| A. | 2-3i | B. | -2-3i | C. | 2+3i | D. | -2+i |
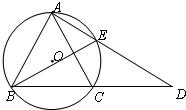 如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.