题目内容
18.在△ABC中,B=60°,b=$\sqrt{3}$,则c+2a的最大值2$\sqrt{7}$.分析 利用余弦定理和已知条件求得a和c的关系,设c+2a=m代入,利用判别大于等于0求得m的范围,则m的最大值可得.
解答 解:由余弦定理cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,
所以a2+c2-ac=b2=3,
设c+2a=m,即c=m-2a,
代入上式得,
7a2-5am+m2-3=0
△=84-3m2≥0,
故m≤2$\sqrt{7}$,当m=2$\sqrt{7}$时,
此时a=$\frac{5\sqrt{7}}{7}$,c=$\frac{4\sqrt{7}}{7}$符合题意.
因此最大值为2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 本题主要考查了余弦定理的应用.涉及了解三角形和函数方程的思想的运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.设i是虚数单位,则复数i3+$\frac{2}{1-i}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
13.设m>1,在约束条件$\left\{\begin{array}{l}{y≥x}\\{x+y≤1}\\{y≤mx+m}\end{array}\right.$下,目标函数z=x+5y的最小值为-8,则m的值为( )
| A. | 3 | B. | $\frac{13}{5}$ | C. | 4 | D. | 8 |
7.复数z满足(z+2)(1+i3)=2(i为虚数单位),则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
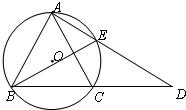 如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.