题目内容
11.在区间(0,1)中随机地取出两个数,则两数之和大于$\frac{2}{3}$的概率是$\frac{7}{9}$.分析 根据题意,设取出的两个数为x、y,分析可得“0<x<1,0<y<1”表示的区域为纵横坐标都在(0,1)之间的正方形区域,易得其面积为1,而x+y>$\frac{2}{3}$表示的区域为直线x+y=$\frac{2}{3}$的上方,且在0<x<1,0<y<1表示区域内部的部分,分别计算其面积,由几何概型的计算公式可得答案.
解答 解:设取出的两个数为x、y;
则有0<x<1,0<y<1,其表示的区域为纵横坐标都在(0,1)之间的正方形区域,易得其面积为1,
而x+y>$\frac{2}{3}$表示的区域为直线x+y=$\frac{2}{3}$的上方,且在0<x<1,0<y<1表示区域内部的部分,
其面积为1-$\frac{1}{2}$×$\frac{2}{3}$×$\frac{2}{3}$=$\frac{7}{9}$,则两数之和大于$\frac{2}{3}$的概率是:$\frac{7}{9}$;
故答案为:$\frac{7}{9}$.
点评 本题考查几何概型的计算,解题的关键在于用平面区域表示出题干的代数关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知函数f(x)=x|x-a|+b,若存在a≤1,使函数f(x)<0对任意x∈[0,1]成立,则实数b的取值范围为( )
| A. | (-∞,2$\sqrt{2}$) | B. | (-∞,-3) | C. | (-$∞,-3+2\sqrt{2}$) | D. | (4+2$\sqrt{2}$,+∞) |
16.在一次数学实验中,运用计算器采集到如下一组数据:
则y关于x的函数关系与下列最接近的函数(其中a、b、c为待定系数)是( )
| x | -2.0 | -1.0 | 0 | 1.0 | 2.0 | 3.0 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
| A. | y=a+bx | B. | y=a+bx | C. | f(x)=ax2+b | D. | y=a+$\frac{b}{x}$ |
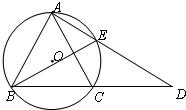 如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.