题目内容
1．已知实数x，y满足不等式$\left\{\begin{array}{l}{y≥x}\\{x+y≤2}\\{x≥a}\end{array}\right.$，且z=2x+y，若x的最大值与最小值之和是6，则实数a的值是1．分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数求得最值，再由最大值与最小值之和是6求得a的值．
解答 解：由约束条件$\left\{\begin{array}{l}{y≥x}\\{x+y≤2}\\{x≥a}\end{array}\right.$作出可行域如图，
由可行域知，目标函数z=2x+y过点A（a，a）时有最小值，最小值为3a，
过B（1，1）时有最大值，最大值为3．
∴由3a+3=6，得a=1．
故答案为：1．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
12．如图，在△OAB中，P为线段AB上的一点，若$\overrightarrow{{O}{P}}$=x$\overrightarrow{{O}{A}}$+y$\overrightarrow{{O}{B}}$，且$\overrightarrow{{B}{P}}$=2$\overrightarrow{{P}{A}}$，则$\frac{x}{y}$等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | 1 | D． | 2 |
9．设i是虚数单位，则复数i3+$\frac{2}{1-i}$=（ ）
| A． | 1 | B． | -1 | C． | i | D． | -i |
16．某几何体的正视图，侧视图及俯视图均如图所示，则该几何体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{6}$ |
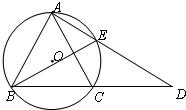如图，⊙O是△ABC的外接圆，AB=AC，延长BC到点D，使得CD=AC，连结AD交⊙O于点E，连结BE，若∠D=35°，则∠ABE的大小为35°．