题目内容
16.已知sinα-cosα=$\frac{1}{2}$,且α∈(0,π),则sinα+cosα=( )| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $-\frac{{\sqrt{7}}}{2}$ | C. | $±\frac{{\sqrt{7}}}{2}$ | D. | $±\frac{1}{2}$ |
分析 由题意利用同角三角函数的基本关系可得sinαcosα=$\frac{3}{8}$>0,可得α为锐角,再根据sinα+cosα=$\sqrt{{(sinα+cosα)}^{2}}$,计算求的结果.
解答 解:∵sinα-cosα=$\frac{1}{2}$,∴1-2sinαcosα=$\frac{1}{4}$,∴sinαcosα=$\frac{3}{8}$>0.
再结合α∈(0,π),可得α为锐角,故sinα+cosα=$\sqrt{{(sinα+cosα)}^{2}}$=$\sqrt{1+2×\frac{3}{8}}$=$\frac{\sqrt{7}}{2}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
7.复数z满足(z+2)(1+i3)=2(i为虚数单位),则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
4.设i为虚数单位,则复数$\frac{5-i}{1+i}$的共轭复数为( )
| A. | 2-3i | B. | -2-3i | C. | 2+3i | D. | -2+i |
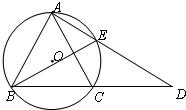 如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.