题目内容
14.已知数列{an}满足:a1=1,an=2an-1+1(n≥2)(1)求证{an+1}是等比数列,并求{an}的通项;
(2)已知bn=log2(an+1),cn=an•bn,求数列|cn|的前n项和Tn.
分析 (1)通过对an=2an-1+1变形可知an+1=2(an-1+1),进而数列{an+1}是首项、公比均为2的等比数列,计算即得结论;
(2)通过(1)可知cn=an•bn=n•2n-n,利用错位相减法计算即得数列{n•2n}的前n项和为Qn,进而计算可得结论.
解答 (1)证明:∵an=2an-1+1,
∴an+1=2(an-1+1),
又∵a1+1=1+1=2,
∴数列{an+1}是首项、公比均为2的等比数列,
∴an+1=2•2n-1=2n,
∴数列{an}的通项an=2n-1;
(2)解:由(1)可知bn=log2(an+1)=$lo{g}_{2}{2}^{n}$=n,
cn=an•bn=(2n-1)•n=n•2n-n,
记数列{n•2n}的前n项和为Qn,
则Qn=1•21+2•22+3•23+…+n•2n,
∴$\frac{1}{2}$Qn=1•20+2•21+3•22+…+(n-1)•2n-2+n•2n-1,
两式相减得:-$\frac{1}{2}$Qn=20+21+22+…+2n-2+2n-1-n•2n
=$\frac{1-{2}^{n}}{1-2}$-n•2n
=-1+(1-n)•2n,
∴Qn=-2•[-1+(1-n)•2n]=2+(n-1)•2n+1,
∴数列{cn}的前n项和Tn=Qn-$\frac{n(n+1)}{2}$=2+(n-1)•2n+1-$\frac{n(n+1)}{2}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
4.已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1.设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.则$\frac{|TF|}{|PQ|}$最小值为( )
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
5.函数y=7tan(-$\frac{1}{2}$x+$\frac{π}{3}$)的最小正周期是( )
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
9.设i是虚数单位,则复数i3+$\frac{2}{1-i}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
19.已知函数f(x)=x|x-a|+b,若存在a≤1,使函数f(x)<0对任意x∈[0,1]成立,则实数b的取值范围为( )
| A. | (-∞,2$\sqrt{2}$) | B. | (-∞,-3) | C. | (-$∞,-3+2\sqrt{2}$) | D. | (4+2$\sqrt{2}$,+∞) |
4.设i为虚数单位,则复数$\frac{5-i}{1+i}$的共轭复数为( )
| A. | 2-3i | B. | -2-3i | C. | 2+3i | D. | -2+i |
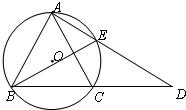 如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.