题目内容

17．已知棱长为$\sqrt{2}$四面体ABCD的各顶点在同一个球面上，则该球的体积为（　　）
A．$\frac{1}{3}$πB．$\frac{2}{3}$πC．$\frac{\sqrt{3}}{2}$πD．3π

分析 把四面体补成正方体，两者的外接球是同一个，求出正方体的棱长，然后求出正方体的对角线长，就是球的直径，即可求出球的体积．

解答 解：如图，将四面体补成正方体，则正方体的棱长是1，
正方体的对角线长为：$\sqrt{3}$，
则此球的体积为：$\frac{4}{3}$π×$（\frac{\sqrt{3}}{2}）^{3}$=$\frac{\sqrt{3}}{2}$π
故选：C．

点评 本题是基础题，考查空间想象能力，正四面体的外接球转化为正方体外接球，使得问题的难度得到降低，问题得到解决，注意正方体的对角线就是球的直径，也是比较重要的．

练习册系列答案
相关题目
19．已知函数f（x）=$\left\{\begin{array}{l}{\frac{7x-3}{2x+2}\\ x∈（\frac{1}{2}，1]}\\{-\frac{1}{3}x+\frac{1}{6}\\ x∈[0，\frac{1}{2}]}\end{array}\right.$，函数g（x）=asin（$\frac{π}{6}$x）-2a+2（a＞0），若存在x1，x2∈[0，1]，使得f（x1）=g（x2）成立，则实数a的取值范围是[$\frac{1}{2}$，$\frac{4}{3}$]．
8．已知a＞0，b＞0，且点（a，b）在直线x+y=2上，则2a+2b的最小值为4．
5．函数y=7tan（-$\frac{1}{2}$x+$\frac{π}{3}$）的最小正周期是（　　）
A．4πB．2πC．πD．$\frac{π}{2}$
12．如图，在△OAB中，P为线段AB上的一点，若$\overrightarrow{{O}{P}}$=x$\overrightarrow{{O}{A}}$+y$\overrightarrow{{O}{B}}$，且$\overrightarrow{{B}{P}}$=2$\overrightarrow{{P}{A}}$，则$\frac{x}{y}$等于（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．1D．2
2．${∫}_{1}^{a}$（3x+$\frac{1}{x}$）dx=$\frac{9}{2}$+ln2（a＞1），则a=2．
9．设i是虚数单位，则复数i3+$\frac{2}{1-i}$=（　　）
A．1B．-1C．iD．-i
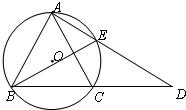6．如图，⊙O是△ABC的外接圆，AB=AC，延长BC到点D，使得CD=AC，连结AD交⊙O于点E，连结BE，若∠D=35°，则∠ABE的大小为35°．
7．复数z满足（z+2）（1+i3）=2（i为虚数单位），则z=（　　）
A．1-iB．1+iC．-1-iD．-1+i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网