题目内容
已知定义在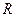 上的奇函数
上的奇函数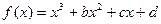 在
在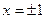 处取得极值.
处取得极值.
(Ⅰ)求函数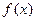 的解析式;
的解析式;
(Ⅱ)试证:对于区间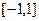 上任意两个自变量的值
上任意两个自变量的值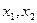 ,都有
,都有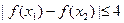 成立;
成立;
(Ⅲ)若过点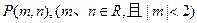 可作曲线
可作曲线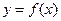 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.
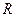 上的奇函数
上的奇函数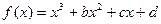 在
在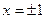 处取得极值.
处取得极值.(Ⅰ)求函数
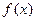 的解析式;
的解析式;(Ⅱ)试证:对于区间
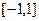 上任意两个自变量的值
上任意两个自变量的值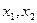 ,都有
,都有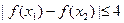 成立;
成立;(Ⅲ)若过点
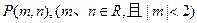 可作曲线
可作曲线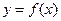 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.(Ⅰ) 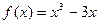 (Ⅲ)8
(Ⅲ)8
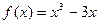 (Ⅲ)8
(Ⅲ)8(I)由题意 ,∴
,∴ ,
,
∴ ,又
,又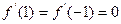 ,
,
即
解得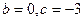 .
.
∴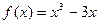 ------------------------------------------------4分
------------------------------------------------4分
(II)∵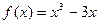 ,
, ,
,
当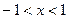 时,
时, ,故
,故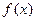 在区间[-1,1]上为减函数,
在区间[-1,1]上为减函数,
∴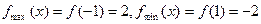
对于区间[-1,1]上任意两个自变量的值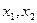 ,
,
∴ -------------------------------9分
-------------------------------9分
(III)设切点为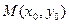 ,则点M的坐标满足
,则点M的坐标满足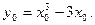
因 ,故切线
,故切线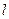 的方程为:
的方程为:
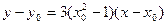 ,
,
∵ ,∴
,∴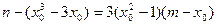
整理得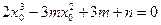 .
.
∵若过点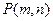 可作曲线
可作曲线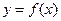 的三条切线,
的三条切线,
∴关于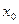 方程
方程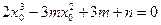 有三个实根.
有三个实根.
设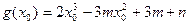 ,则
,则
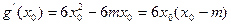 ,
,
由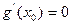 ,得
,得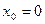 或
或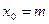 .
.
由对称性,先考虑
∵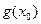 在
在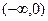 ,
,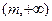 上单调递增,在
上单调递增,在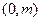 上单调递减.
上单调递减.
∴函数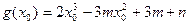 的极值点为
的极值点为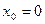 ,或
,或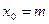
∴关于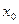 方程
方程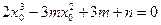 有三个实根的充要条件是
有三个实根的充要条件是
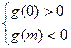 ,解得
,解得 .
.
故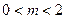 时,点P对应平面区域的面积
时,点P对应平面区域的面积
故 时,所求点P对应平面区域的面积为
时,所求点P对应平面区域的面积为 ,即8.
,即8.
 ,∴
,∴ ,
,∴
 ,又
,又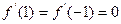 ,
,即

解得
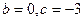 .
.∴
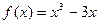 ------------------------------------------------4分
------------------------------------------------4分(II)∵
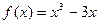 ,
, ,
,当
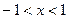 时,
时, ,故
,故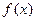 在区间[-1,1]上为减函数,
在区间[-1,1]上为减函数,∴
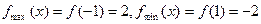
对于区间[-1,1]上任意两个自变量的值
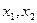 ,
,∴
 -------------------------------9分
-------------------------------9分(III)设切点为
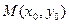 ,则点M的坐标满足
,则点M的坐标满足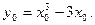
因
 ,故切线
,故切线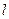 的方程为:
的方程为: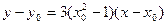 ,
,∵
 ,∴
,∴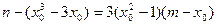
整理得
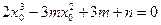 .
.∵若过点
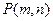 可作曲线
可作曲线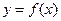 的三条切线,
的三条切线,∴关于
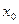 方程
方程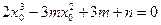 有三个实根.
有三个实根.设
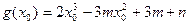 ,则
,则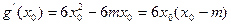 ,
,由
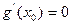 ,得
,得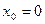 或
或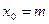 .
.由对称性,先考虑

∵
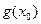 在
在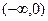 ,
,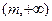 上单调递增,在
上单调递增,在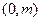 上单调递减.
上单调递减.∴函数
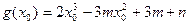 的极值点为
的极值点为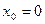 ,或
,或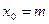
∴关于
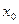 方程
方程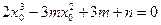 有三个实根的充要条件是
有三个实根的充要条件是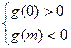 ,解得
,解得 .
.故
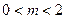 时,点P对应平面区域的面积
时,点P对应平面区域的面积
故
 时,所求点P对应平面区域的面积为
时,所求点P对应平面区域的面积为 ,即8.
,即8.
练习册系列答案
相关题目
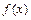 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,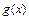 的图象与
的图象与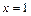 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,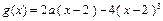 .
.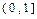 上为增函数,求
上为增函数,求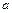 的取值范围;
的取值范围;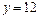 上?若存在,求出
上?若存在,求出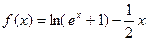 .
.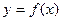 的单调区间,并判断函数的奇偶性;
的单调区间,并判断函数的奇偶性;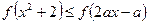 的解集是集合
的解集是集合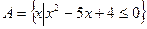 的子集,求实数
的子集,求实数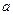 的取值范围.
的取值范围.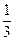 ,1),求函数f(x)的解析式;
,1),求函数f(x)的解析式;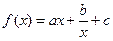 (
(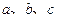 是常数)是奇函数,且满足
是常数)是奇函数,且满足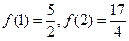 ,
,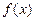 在区间
在区间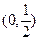 上的单调性并说明理由;
上的单调性并说明理由;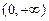 上的最小值.
上的最小值.
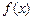 的定义域为
的定义域为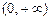 ,
,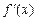 ,且对任意正数
,且对任意正数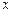 均有
均有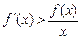 ,
,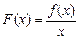 在
在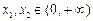 ,比较
,比较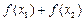 与
与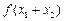 的大小,并证明你的结论;
的大小,并证明你的结论;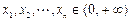 ,若
,若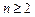 ,比较
,比较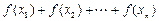 与
与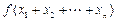 的大小,并证明你的结论.
的大小,并证明你的结论.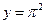 ,则
,则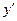 等于( )
等于( )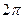
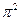
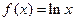 ,
,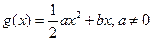 。
。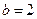 ,且函数
,且函数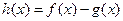 存在单调递减区间,求
存在单调递减区间,求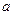 的取值范围;
的取值范围;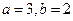 时,求函数
时,求函数