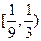题目内容
已知在函数 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为
(Ⅰ)求m、n的值;
(Ⅱ)是否存在最小的正整数k,使得不等式 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
(Ⅲ)(文科不做)求证:
 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为
(Ⅰ)求m、n的值;
(Ⅱ)是否存在最小的正整数k,使得不等式
 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;(Ⅲ)(文科不做)求证:

(1) (2)存在最小的正整数k=2007,使得不等式
(2)存在最小的正整数k=2007,使得不等式 恒成立(3)见解析
恒成立(3)见解析
 (2)存在最小的正整数k=2007,使得不等式
(2)存在最小的正整数k=2007,使得不等式 恒成立(3)见解析
恒成立(3)见解析(Ⅰ) 依题意,得
依题意,得
∴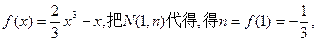 ∴
∴ ………………2分
………………2分
(Ⅱ)令
当 在此区间为增函数
在此区间为增函数
当 在此区间为减函数
在此区间为减函数
当 在此区间为增函数
在此区间为增函数
 处取得极大值………………5分
处取得极大值………………5分
又
因此,当 …………6分
…………6分
要使得不等式
所以,存在最小的正整数k=2007,使得不等式 恒成立。7分
恒成立。7分
(Ⅲ)(方法一)


 ……………10分 又∵
……………10分 又∵ ∴
∴
∴

综上可得 ………12分
………12分
(方法2)由(2)知,函数
上是减函数,在[ ,1]上是增函数, 又
,1]上是增函数, 又
所以,当 时,-
时,- …………9分
…………9分


 ……10分
……10分
又t>0, ,且函数
,且函数 上是增函数,
上是增函数,

综上可得 ………………12分
………………12分
 依题意,得
依题意,得
∴
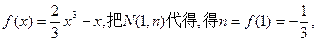 ∴
∴ ………………2分
………………2分(Ⅱ)令

当
 在此区间为增函数
在此区间为增函数当
 在此区间为减函数
在此区间为减函数当
 在此区间为增函数
在此区间为增函数 处取得极大值………………5分
处取得极大值………………5分又

因此,当
 …………6分
…………6分要使得不等式

所以,存在最小的正整数k=2007,使得不等式
 恒成立。7分
恒成立。7分(Ⅲ)(方法一)



 ……………10分 又∵
……………10分 又∵ ∴
∴
∴


综上可得
 ………12分
………12分(方法2)由(2)知,函数

上是减函数,在[
 ,1]上是增函数, 又
,1]上是增函数, 又
所以,当
 时,-
时,- …………9分
…………9分

 ……10分
……10分又t>0,
 ,且函数
,且函数 上是增函数,
上是增函数,
综上可得
 ………………12分
………………12分
练习册系列答案
相关题目
 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,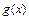 的图象与
的图象与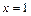 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,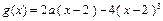 .
.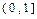 上为增函数,求
上为增函数,求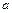 的取值范围;
的取值范围;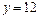 上?若存在,求出
上?若存在,求出 .
.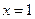 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出 关于
关于 的关系式(用
的关系式(用 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求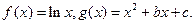
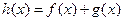 是单调递增函数,求实数
是单调递增函数,求实数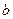 的取值范围;
的取值范围;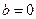 时,两曲线
时,两曲线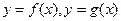 有公共点P,设曲线
有公共点P,设曲线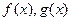 在P处的切线分别为
在P处的切线分别为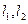 ,若切线
,若切线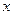 轴围成一个等腰三角形,求P点坐标和
轴围成一个等腰三角形,求P点坐标和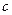 的值;
的值;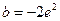 时,讨论关于
时,讨论关于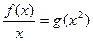 的根的个数
的根的个数
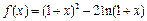 .
.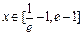 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;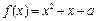 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.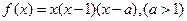
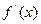 ; 并证明
; 并证明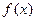 有两个不同的极值点
有两个不同的极值点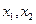 ;
; 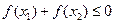 成立,求
成立,求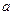 的取值范围.
的取值范围.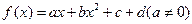 的导函数
的导函数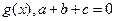 ,且
,且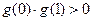 设
设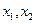 是方程
是方程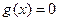 的两根,则|
的两根,则|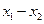 |的取值范围为
|的取值范围为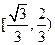 B
B 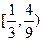 C
C 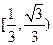 D
D