题目内容
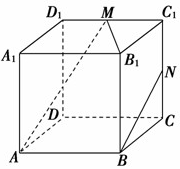
正方体A-C1中,棱长为1,M在棱AB上,AM=1/3,P是面ABCD上的动点,P到线A1D1的距离与P到点M的距离平方差为1,则P点的轨迹以下哪条曲线上? ( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
D
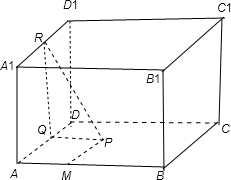
解:如图所示:正方体ABCD-A1B1C1D1中,作PQ⊥AD,Q为垂足,则PQ⊥面ADD1A1,过点Q作QR⊥D1A1,
则D1A1⊥面PQR,PR即为点P到直线A1D1的距离,由题意可得 PR2-PQ2=RQ2=4.
又已知 PR2-PM2=4,
∴PM=PQ,即P到点M的距离等于P到AD的距离,根据抛物线的定义可得,点P的轨迹是抛物线,
故选D.

练习册系列答案
相关题目
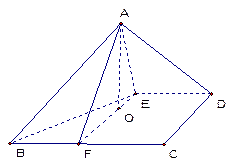
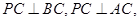 点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。
点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。 平面ABC
平面ABC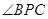 是直线EF与直线PC所成的角
是直线EF与直线PC所成的角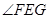 是平面PAB与平面ABC所成二面角的平面角
是平面PAB与平面ABC所成二面角的平面角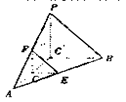
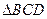 中,
中,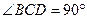 ,
,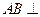 平面
平面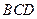 ,
,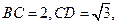
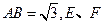 分别为
分别为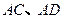 上的动点.
上的动点.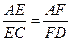 ,求证:平面
,求证:平面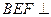 平面
平面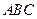 ;
;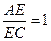 ,
,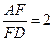 ,求平面
,求平面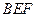 与平面
与平面
 3分)如图6,正方形
3分)如图6,正方形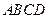 所在平面与圆
所在平面与圆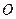 所在平面相交于
所在平面相交于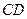 ,
,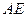 垂直于圆
垂直于圆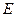 是圆
是圆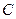 、
、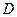 的点,
的点,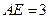 ,圆
,圆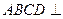 平面
平面 ;
;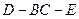 的平面角的正切值.
的平面角的正切值.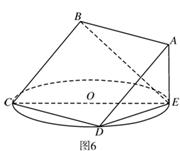
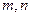 是两条不同的直线,
是两条不同的直线,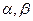 是两个不同的平面,
是两个不同的平面, 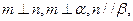 则
则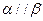
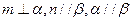 ,则
,则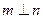
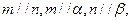 则
则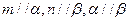 ,则
,则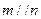
 AB-C2为60o,
AB-C2为60o, 则点C
则点C 1与C2之间的距离可能是___________.(写出二个可能值即可)
1与C2之间的距离可能是___________.(写出二个可能值即可)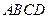 中,
中,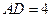 ,
,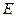 、
、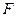 分别是
分别是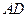 、
、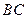 的中点,点
的中点,点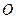 在
在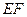 上,且
上,且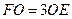 ,把
,把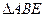 沿着
沿着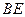 翻折,使点
翻折,使点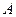 在平面
在平面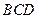 上的射影恰为点
上的射影恰为点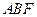
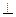
 平面
平面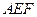 ;
;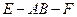 的大小.
的大小.