题目内容
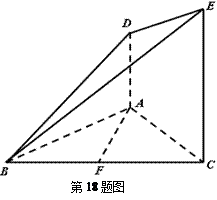
如图,在三棱锥P—ABC中,已知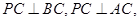 点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。
点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。
①平面EFG//平面PBC
②平面EFG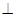 平面ABC
平面ABC
③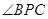 是直线EF与直线PC所成的角
是直线EF与直线PC所成的角
④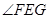 是平面PAB与平面ABC所成二面角的平面角
是平面PAB与平面ABC所成二面角的平面角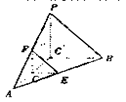
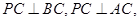 点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。
点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。①平面EFG//平面PBC
②平面EFG
 平面ABC
平面ABC③
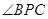 是直线EF与直线PC所成的角
是直线EF与直线PC所成的角④
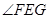 是平面PAB与平面ABC所成二面角的平面角
是平面PAB与平面ABC所成二面角的平面角
①②③
考查知识点:本题考查立体几何中的面面的平行和垂直的判定应用,以及面面、线线的夹角问题。
解析: 如图
 E、F、G分别为各棱的中点
E、F、G分别为各棱的中点 FG//PC,
FG//PC,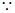 PC
PC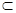 面PBC,
面PBC, FG//面PBC,
FG//面PBC,同理,GE//面PBC,
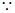 FG
FG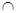 GE=点G,
GE=点G, 面EFG//面PBC,故选①;
面EFG//面PBC,故选①;又
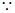
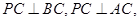
 PC
PC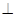 面ABC,且FG
面ABC,且FG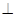 PC,
PC, FG
FG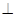 面ABC,
面ABC, 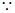 FG
FG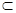 面EFG,
面EFG, 面EFG
面EFG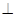 面ABC故选②;
面ABC故选②;又易知EF//BP,故
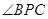 是直线EF与直线PC所成的角,选③
是直线EF与直线PC所成的角,选③当
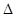 ABC为直角三角形时④选项才正确。
ABC为直角三角形时④选项才正确。所以选①②③

练习册系列答案
相关题目
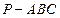 中,
中,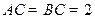 ,
,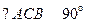 ,侧面
,侧面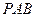 为等边三角形,侧棱
为等边三角形,侧棱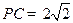 .
.
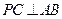 ;
;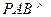 平面
平面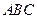 ;
;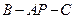 的余弦值
的余弦值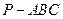 的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥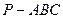 中,
中,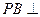 底面
底面 于
于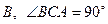 ,
,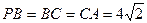 ,点
,点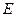 ,点
,点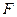 分别是
分别是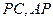 的中点.
的中点.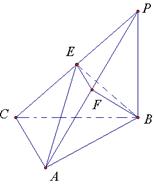
 ⊥侧面
⊥侧面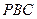 ;
;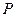 到平面
到平面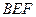 的距离;
的距离;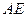 与
与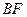 所成的角的余弦.
所成的角的余弦.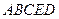 中,
中,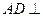 平面
平面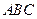 ,
,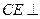 平面
平面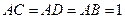 ,
,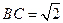 ,
,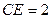 ,
,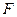 为
为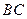 的中点.
的中点.
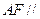 平面
平面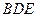 ;
;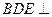 平面
平面 .
.
 关于直线
关于直线 对称,
对称,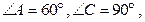
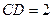 .
.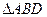 沿
沿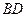 折起(如图二),使二面角
折起(如图二),使二面角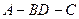 的余弦值等于
的余弦值等于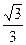 .对于图二,
.对于图二,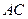 ;
;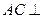 平面
平面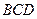 ;
;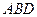 所成角的正弦值.
所成角的正弦值.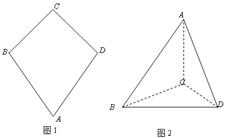
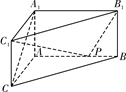
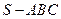 中,
中,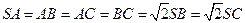 ,
,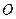 为
为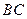 的中点.
的中点.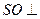 面
面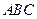 ;
;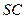 与
与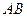 所成角的余弦值.
所成角的余弦值.