题目内容
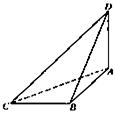
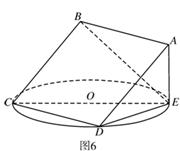
(本小题满分1 3分)如图6,正方形
3分)如图6,正方形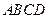 所在平面与圆
所在平面与圆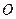 所在平面相交于
所在平面相交于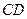 ,
,
线段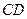 为圆
为圆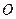 的弦,
的弦,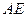 垂直于圆
垂直于圆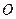 所在平面,
所在平面,
垂足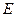 是圆
是圆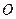 上异于
上异于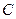 、
、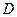 的点,
的点,
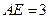 ,圆
,圆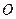 的直径为9.
的直径为9.
(1)求证:平面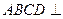 平面
平面 ;
;
(2)求二面角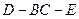 的平面角的正切值.
的平面角的正切值.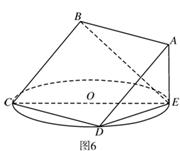
 3分)如图6,正方形
3分)如图6,正方形 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于 ,
,线段
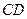 为圆
为圆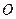 的弦,
的弦,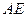 垂直于圆
垂直于圆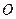 所在平面,
所在平面,垂足
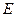 是圆
是圆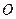 上异于
上异于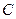 、
、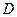 的点,
的点,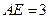 ,圆
,圆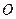 的直径为9.
的直径为9.(1)求证:平面
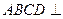 平面
平面 ;
;(2)求二面角
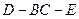 的平面角的正切值.
的平面角的正切值.
(1)略
(2)
(1)证明:∵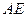 垂直于圆
垂直于圆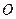 所在平面,
所在平面,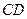 在圆
在圆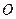 所在平面上,∴
所在平面上,∴
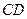 .
.

在正方形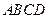 中,
中,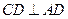 ,
,
∵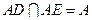 ,∴
,∴ 平面
平面 .∵
.∵ 平面
平面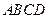 ,
,
∴平面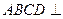 平面
平面
 . …………4分
. …………4分
(2)解法1:∵ 平面
平面 ,
,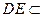 平面
平面 ,
,
∴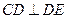 .
.

过点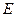 作
作 于点
于点 ,作
,作 交
交 于点
于点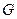 ,连结
,连结 ,
,
 由于
由于 平面
平面 ,
, 平面
平面 ,
,
∴ .∵
.∵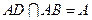 ,∴
,∴ 平面
平面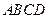 .
.
∵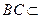 平面
平面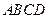 ,∴
,∴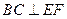 .
.
∵ ,
,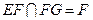 ,∴
,∴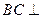 平面
平面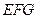 .
.
∵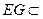 平面
平面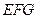 ,∴
,∴ .
.
∴ 是二面角
是二面角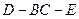 的平面角.
的平面角.
在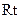 △
△ 中,
中, ,
,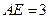 ,
, ,
,
∵ ,∴
,∴ .
.
在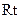 △
△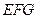 中,
中,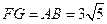 ,
,
∴ .故二面角
.故二面角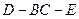 的平面角的正切值为
的平面角的正切值为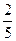 . …
. … ………13分
………13分
解法2:∵ 平面
平面 ,
,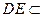 平面
平面 ,
,
∴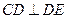 .∴
.∴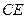
 为圆
为圆 的直径,即
的直径,即 . 设正方形
. 设正方形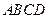 的边长为
的边长为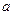 ,
,
 在
在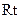 △
△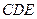 中,
中,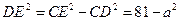 ,
,
在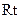 △
△
 中,
中,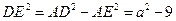 ,
,
由 ,解得,
,解得, .∴
.∴ .
.
设平面 的法向量为
的法向量为 ,
,
则 即
即
取 ,则
,则 是平面
是平面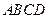 的一个法向量.
的一个法向量.
∵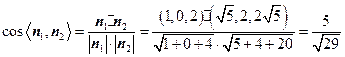 ,
,
∴ .∴
.∴ .故二面角
.故二面角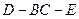 的平面角的正切值为
的平面角的正切值为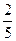 .
.
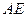 垂直于圆
垂直于圆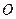 所在平面,
所在平面,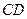 在圆
在圆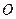 所在平面上,∴
所在平面上,∴
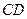 .
. 
在正方形
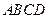 中,
中,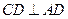 ,
,∵
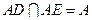 ,∴
,∴ 平面
平面 .∵
.∵ 平面
平面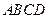 ,
,∴平面
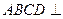 平面
平面
 . …………4分
. …………4分(2)解法1:∵
 平面
平面 ,
,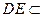 平面
平面 ,
,∴
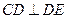 .
. 
过点
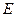 作
作 于点
于点 ,作
,作 交
交 于点
于点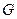 ,连结
,连结 ,
, 由于
由于 平面
平面 ,
, 平面
平面 ,
,∴
 .∵
.∵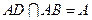 ,∴
,∴ 平面
平面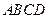 .
.∵
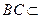 平面
平面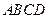 ,∴
,∴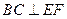 .
.∵
 ,
,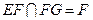 ,∴
,∴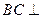 平面
平面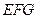 .
.∵
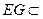 平面
平面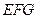 ,∴
,∴ .
.∴
 是二面角
是二面角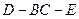 的平面角.
的平面角.在
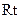 △
△ 中,
中, ,
,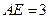 ,
, ,
,∵
 ,∴
,∴ .
. 在
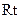 △
△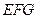 中,
中,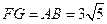 ,
,∴
 .故二面角
.故二面角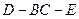 的平面角的正切值为
的平面角的正切值为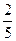 . …
. … ………13分
………13分解法2:∵
 平面
平面 ,
,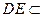 平面
平面 ,
,∴
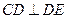 .∴
.∴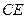
 为圆
为圆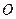 的直径,即
的直径,即 . 设正方形
. 设正方形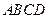 的边长为
的边长为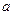 ,
, 在
在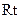 △
△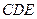 中,
中,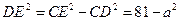 ,
,在
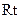 △
△
 中,
中,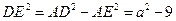 ,
,由
 ,解得,
,解得, .∴
.∴ .
. 设平面
 的法向量为
的法向量为 ,
,则
 即
即
取
 ,则
,则 是平面
是平面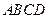 的一个法向量.
的一个法向量.∵
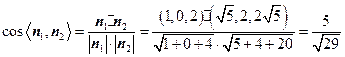 ,
, ∴
 .∴
.∴ .故二面角
.故二面角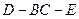 的平面角的正切值为
的平面角的正切值为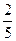 .
.
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
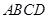 中,截面
中,截面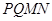 是正方形,则在下列命题中,错误的为( )
是正方形,则在下列命题中,错误的为( )
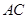 ∥截面
∥截面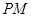 与
与 所成的角为
所成的角为
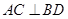
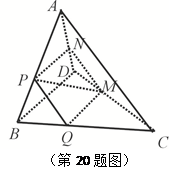
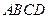 所在平面与圆
所在平面与圆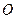 所在平面相交于
所在平面相交于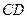 ,线段
,线段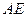 垂直于圆
垂直于圆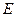 是圆
是圆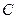 、
、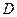 的点,
的点,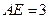 ,圆
,圆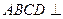 平面
平面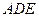 ;
;
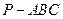 的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
的四个顶点均在半径为3的球面上,且PA、PB、PC两两互相垂直,则三棱锥
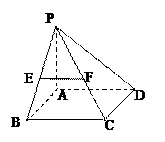
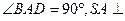 底面ABCD,SA=AB=BC=2,SD与平面ABCD所成角的正切值为
底面ABCD,SA=AB=BC=2,SD与平面ABCD所成角的正切值为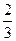 。
。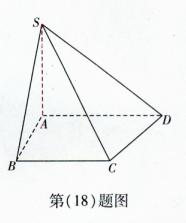
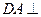 平面ABC,
平面ABC,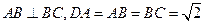 ,则球O的体积等于 。
,则球O的体积等于 。