题目内容
16.已知(2x-1)7=a0+a1x+a2x2+…+a7x7,则a1+a2+…a7=2.分析 在所给的等式中,令x=0可得a0=-1;再令x=1,可得a0+a1+a2+…a7=1,由此求得 a1+a2+…a7的值.
解答 解:在(2x-1)7=a0+a1x+a2x2+…+a7x7 中,令x=0可得a0=-1.
再令x=1,可得a0+a1+a2+…a7=1,可得 a1+a2+…a7=2,
故答案为:2.
点评 本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.为了调查胃病是否与生活规律有关,某同学在当地随机调查了500名30岁以上的人,并根据调查结果计算出了随机变量K2的观测值k=6.080,则认为30岁以上的人患胃病与生活无规律有关时,出错的概率不会超过( )
附表:
附表:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.001 | B. | 0.005 | C. | 0.010 | D. | 0.025 |
11.从4名教师和3名学生中选出4人参加座谈会,若选出的4人中既有教师也有学生,则不同的选法种数为( )
| A. | 140 | B. | 120 | C. | 35 | D. | 34 |
1.甲、乙两位射击运动员在一次射击测试中各射靶10次,两人射中环数统计结果如图所示:
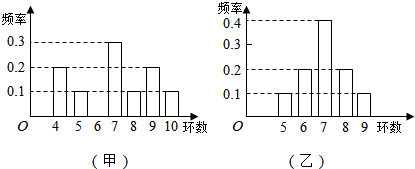
若用$\overline{x}$表示所得环数的平均数,s表示标准差,则下列结论正确的是( )

若用$\overline{x}$表示所得环数的平均数,s表示标准差,则下列结论正确的是( )
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$ | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | D. | s甲<s乙 |
8.某住宅小区有高中生27人,初中生54人,小学生81人,为了了解他们的身体健康状况,需要从中抽取一个容量为36的样本,用分层抽样的方法分别从高中生、初中生、小学生中各抽取的人数为( )
| A. | 18,12,6 | B. | 12,6,8 | C. | 18,6,12 | D. | 6,12,18 |