题目内容
11.函数 f(x)=(x-2014)(x+2015)的图象与x轴,y轴有三个交点,有一个圆恰经过这三个点,则此圆与坐标轴的另一个交点是( )| A. | (0,-1) | B. | (0,1) | C. | (0,$\sqrt{2014×2015}$) | D. | (0,$\sqrt{\frac{2014}{2015}}$) |
分析 先求出f(x)的图象与x轴的交点M、N的坐标,f(x)的图象与y轴的交点P的坐标,再利用圆的弦的性质求得此圆与坐标轴的另一个交点R的坐标.
解答 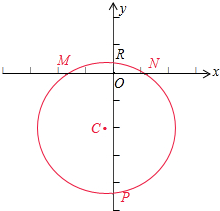 解:函数 f(x)=(x-2014)(x+2015)的图象与x轴的交点
解:函数 f(x)=(x-2014)(x+2015)的图象与x轴的交点
分别为M(-2015,0)、N(2014,0),
f(x)的图象与y轴的交点P(0,-2014×2015),
故圆心的横坐标为$\frac{-2015+2014}{2}$=-$\frac{1}{2}$.
设圆心C(-$\frac{1}{2}$,b),由CN=CP可得,
${(-\frac{1}{2}-2014)}^{2}$+b2=$\frac{1}{4}$+(b+2014×2015)2,
求得b=$\frac{1}{2}$-1007×2015,即圆心C(-$\frac{1}{2}$,$\frac{1}{2}$-1007×2015 ).
设此圆与坐标轴的另一个交点是为R(0,m),则根据圆的弦的性质可得$\frac{1}{2}$-1007×2015=$\frac{m+(-2014×2015)}{2}$,求得m=1,
故选:B.
点评 本题主要考查直线和圆相交的性质,圆的弦的性质,体现了数形结合以及转化的数学思想,属于中档题.

练习册系列答案
相关题目
2.设全集U=R,集合A={x|x-1>0},B={x|-x2+2x≤0},则A∩(CUB}=( )
| A. | {x|0<x≤1} | B. | {x|1≤x<1} | C. | {x|1<x<2} | D. | {x|1<x≤1} |
16.△ABC中,a=$\sqrt{7}$,b=3,c=2,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
3.下列程序框表示一个算法输入和输出信息的是( )
| A. |  | B. |  | C. |  | D. |  |

 某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.