题目内容
9．若将函数f（x）=x5表示为：f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4+a5（1+x）5，其中a0，a1，a2，…，a5为实数，则a3=10．分析 把f（x）=[-1+（1+x）]5 按照二项式定理展开，结合已知f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4+a5（1+x）5，求得a3的值．
解答 解：f（x）=x5=[-1+（1+x）]5=-${C}_{5}^{0}$+${C}_{5}^{1}$•（1+x）-${C}_{5}^{2}$•（1+x）2+${C}_{5}^{3}$•（1+x）3-${C}_{5}^{4}$•（1+x）4+${C}_{5}^{5}$•（1+x）5，
再根据f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4+a5（1+x）5，
可得a3=${C}_{5}^{3}$=10，
故答案为：10．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
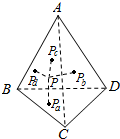在平面内，可以用面积法证明下面的结论：从三角形内部任意一点，向各边引垂线，其长度分别为pa，pb，pc，且相应各边上的高分别为ha，hb，hc，则有$\frac{{p}_{a}}{{h}_{a}}+\frac{{p}_{b}}{{h}_{b}}+\frac{{p}_{c}}{{h}_{c}}$=1．
