题目内容
10.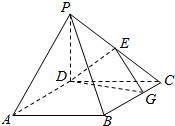 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB(1)求证:PC⊥BC;
(2)求三棱锥C-DEG的体积;
(3)AD边上是否存在一点M,使得PA∥平面MEG?若存在,求AM的长;否则,说明理由.
分析 (1)证明PD⊥BC.BC⊥CD.推出BC⊥平面PCD.然后证明PC⊥BC.
(2)说明GC是三棱锥G-DEC的高.求出S△EDC.然后通过VC-DEG=VG-DEC,求解几何体的体积.
(3)连结AC,取AC中点O,连结EO、GO,延长GO交AD于点M,则PA∥平面MEG.利用直线与平面平行的判定定理证明.通过△OCG≌△OAM,求解所求AM的长.
解答 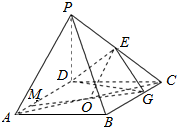 解:(1)证明:∵PD⊥平面ABCD,∴PD⊥BC.又∵ABCD是正方形,∴BC⊥CD.
解:(1)证明:∵PD⊥平面ABCD,∴PD⊥BC.又∵ABCD是正方形,∴BC⊥CD.
又∵PD∩CD=D,∴BC⊥平面PCD.又∵PC?平面PCD,∴PC⊥BC.----------------4
(2)∵BC⊥平面PCD,
∴GC是三棱锥G-DEC的高.
∵E是PC的中点,
∴S△EDC=$\frac{1}{2}$S△PDC=$\frac{1}{2}×\frac{1}{2}PD•DC$=$\frac{1}{2}$×($\frac{1}{2}$×2×2)=1.
∴VC-DEG=VG-DEC=$\frac{1}{3}$GC•S△DEC=$\frac{1}{3}$×$\frac{2}{3}$×1=$\frac{2}{9}$.-----------------------------8
(3)连结AC,取AC中点O,连结EO、GO,延长GO交AD于点M,则PA∥平面MEG.
证明:∵E为PC的中点,O是AC的中点,∴EO∥PA.又∵EO?平面MEG,PA?平面MEG,
∴PA∥平面MEG.
在正方形ABCD中,∵O是AC的中点,BC=PD=2,CG=$\frac{1}{3}$CB.
∴△OCG≌△OAM,∴AM=CG=$\frac{2}{3}$,∴所求AM的长为$\frac{2}{3}$.----------------------------12
点评 本题考查直线与平面平行,几何体的体积的求法,距离公式的应用,考查空间想象能力以及逻辑推理能力计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | {x|0<x≤1} | B. | {x|1≤x<1} | C. | {x|1<x<2} | D. | {x|1<x≤1} |


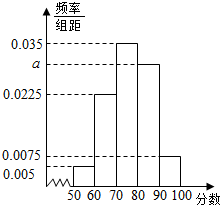 某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.