题目内容
3.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,(2$\overrightarrow{a}$-3$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=61(1)求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ;
(2)求向量$\overrightarrow{a}$+$\overrightarrow{b}$在向量$\overrightarrow{b}$方向上的投影.
分析 (1)利用已知求$\overrightarrow{a}$与$\overrightarrow{b}$的数量积,再利用数量积公式得到向量的夹角;
(2)根据向量投影的定义解答.
解答 解:(1)因为:|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,(2$\overrightarrow{a}$-3$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=61,
所以$4{\overrightarrow{a}}^{2}-3{\overrightarrow{b}}^{2}-4\overrightarrow{a}•\overrightarrow{b}$=61,即64-27-4$\overrightarrow{a}•\overrightarrow{b}$=61,所以$\overrightarrow{a}•\overrightarrow{b}=-6$,
所以cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-6}{4×3}=-\frac{1}{2}$,
所以$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ为120°;
(2)向量$\overrightarrow{a}$+$\overrightarrow{b}$在向量$\overrightarrow{b}$方向上的投影$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$=$\frac{-6+9}{3}$=1.
点评 本题考查了向量数量积公式的运用求向量的夹角以及求向量的投影;熟练掌握数量积公式是关键.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
| A. | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\overrightarrow b=\overrightarrow c$ | B. | 若$\overrightarrow a=(1,k)$,$\overrightarrow b=(-2,6)$,$\overrightarrow a∥$$\overrightarrow b$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow a•\overrightarrow b=0$ | D. | 若$\overrightarrow a$与$\overrightarrow b$是单位向量,则$\overrightarrow a•\overrightarrow b=1$. |
| x | 1 | 2 | 3 | 4 | 5 |
| y | 0.5 | 0.9 | 2.1 | 3.0 | 3.5 |
| A. | $z=\sqrt{5}$ | B. | z=5i | C. | $z=\sqrt{3}+\sqrt{2}i$ | D. | z=-1-2i |
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
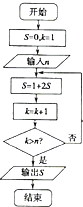 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S=15,那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S=15,那么n的值为( )