题目内容
4.如图几何体中,正视图、侧视图都为长方形的几何体有( )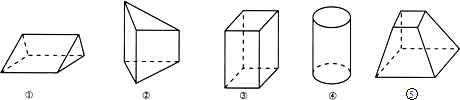
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 逐一分析5个几何体的正视图、侧视图是否为长方形,最后综合分析结果,可得答案.
解答 解:在下列几何体中,
①的正视图为长方形、侧视图为三角形;
②的正视图为梯形、侧视图为梯形;
③的正视图为长方形、侧视图为长方形;
④的正视图为长方形、侧视图为长方形;
⑤的正视图为梯形、侧视图为梯形;
故正视图、侧视图都为长方形的几何体有③④,共2个,
故选:B.
点评 本题考查的知识点是简单空间几何体的三视图,熟练掌握各种简单空间几何体的三视图形状是解答的关键.

练习册系列答案
相关题目
3.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°,则$\vec b•(\vec b-\vec a)$等于( )
| A. | 1 | B. | 3 | C. | 2-$\sqrt{3}$ | D. | 4-$\sqrt{3}$ |
1.已知f(x)=sin(2x-$\frac{π}{4}$),则f(x)的最小正周期和一个单调增区间分别为( )
| A. | π,[-$\frac{π}{4}$,$\frac{π}{4}$] | B. | π,[-$\frac{π}{8}$,$\frac{3π}{8}$] | C. | 2π,[-$\frac{π}{4}$,$\frac{3π}{4}$] | D. | 2π,[-$\frac{π}{4}$,$\frac{π}{4}$] |
9.将f(x)=sinx向左平移$\frac{π}{2}$个单位,得到函数y=g(x)的图象,则下列说法正确的是( )
| A. | y=g(x) 是奇函数 | B. | y=g(x)的周期为π | ||
| C. | y=g(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=g(x)的图象关于点($\frac{π}{2}$-,0)对称 |
16.已知$sinx=\frac{{\sqrt{3}}}{3}$,$x∈({\frac{π}{2},\;π})$,则x等于( )
| A. | $\frac{π}{2}+arcsin\frac{{\sqrt{3}}}{3}$ | B. | $α≠\frac{kπ}{2}(k∈Z)$ | C. | $arcsin\frac{{\sqrt{3}}}{3}$ | D. | $π-arcsin\frac{{\sqrt{3}}}{3}$ |
14.已知复数z=$\frac{{i+{i^2}+{i^3}+{i^4}+…+{i^9}}}{1+i}$,(i为虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |