题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() ,
,![]() (
(![]() )处导数相等,证明:
)处导数相等,证明:![]() ;
;
(2)是否存在![]() ,使直线
,使直线![]() 是曲线
是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线,而且这样的直线
的切线,而且这样的直线![]() 是唯一的,如果存在,求出直线
是唯一的,如果存在,求出直线![]() 方程,如果不存在,请说明理由.
方程,如果不存在,请说明理由.
【答案】(1)见解析(2)存在,![]()
【解析】
(1)求导![]() ,则
,则![]() ,化简得到
,化简得到![]() ,再利用均值不等式到答案.
,再利用均值不等式到答案.
(2)先设切点求切线方程,再根据切线重合得关于一个切点横坐标的函数,利用导数研究函数只有一个零点的情况,即得答案.
(1)当![]() 时,
时,![]() ,所以
,所以![]() ,
,
由题意,得![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() .
.
(2)曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:
![]() ,
,
函数![]() 在点
在点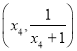 处的切线方程
处的切线方程 ,
,
要存在直线![]() ,使
,使![]() 是曲线
是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线,
的切线,
只需在![]() 处使
处使![]() 与
与![]() 重合,
重合,
所以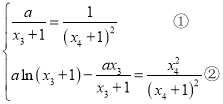
由①得![]() 代入②整理得
代入②整理得![]() ,
,
设![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
则![]() ,设
,设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() .
.
(ⅰ)当![]() 时,
时,![]() ,所以
,所以![]() ,
,
此时![]() ,所以方程
,所以方程![]() 有唯一解
有唯一解![]() ,
,
即![]() ,此时切线方程为
,此时切线方程为![]() ;
;
(ⅱ)当![]() 且
且![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
故![]() 函数单调递增,当
函数单调递增,当![]() 时,函数单调递减,故
时,函数单调递减,故![]() ,
,
故![]() ,同理可证
,同理可证![]() ,
,![]() 成立.
成立.
因为![]() ,则
,则![]()
![]()
![]()
![]() .
.
又由当![]() 时,
时,![]() ,可得
,可得![]() ,
,
则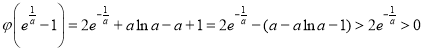 ,
,
所以函数![]() 有两个零点,
有两个零点,
即方程![]() 有两个根
有两个根![]() ,
,![]() ,
,
即![]() ,此时
,此时![]() ,
,![]() ,则
,则![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以直线
,所以直线![]() 不唯一.
不唯一.
综上所述,存在![]() ,使
,使![]() 是曲线
是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线,而且这样的直线
的切线,而且这样的直线![]() 是唯一的.
是唯一的.

【题目】1772年德国的天文学家波得发现了求太阳的行星距离的法则,记地球距离太阳的平均距离为10,可以算得当时已知的六大行星距离太阳的平均距离如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
与太阳的距离 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星与太阳的距离都满足波得定则(某一数列规律),当时德国数学家高斯根据此定则推算,火星和木星之间距离太阳28还有一颗大行星,1801年,意大利天文学家皮亚齐经过观测,果然找到了火星和木星之间距离太阳28的谷神星以及它所在的小行星带,请你根据这个定则,估算从水星开始由近到远算,第10个行星与太阳的平均距离大约是( )
A.388B.772C.1540D.3076