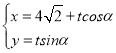Question

【题目】直线l的参数方程为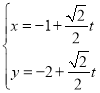（t为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ＝4acosθ，直线l与曲线C交于不同的两点M，N．

（1）求实数a的取值范围；

（2）已知a＞0，设点P（﹣1，﹣2），若|PM|，|MN|，|PN|成等比数列，求a的值．

Answer 1

【答案】（1）（﹣∞，﹣1）∪（0，+∞）．（2）a．

【解析】

（1）转化出直线l的普通方程：y＝x﹣1，曲线C的普通方程：y2＝4ax，联立方程组令即可得解；

（2）设M，N分别对应t1，t2，转化条件得，

，解出方程即可得解.

（1）∵直线l的参数方程为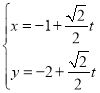（t为参数），

∴直线l的普通方程为：y＝x﹣1，

∵曲线C的极坐标方程为ρsin2θ＝4acosθ，

∴曲线C的普通方程为：y2＝4ax，

联立，得y2＝4a（y+1），即y2﹣4ay﹣4a＝0，

∵直线l与曲线C交于不同的两点M，N，

∴由题知＝（﹣4a）2﹣4（﹣4a）＝16a2+16a＞0，

解得a＜-1或a＞0，

∴实数a的取值范围是（﹣∞，﹣1）∪（0，+∞）．

（2）设M，N分别对应t1，t2，

则有()2＝4a×(t-1)，∴，

由题知|MN|2＝|PM|×|PN|，

由韦达定理有：（t1﹣t2)2＝|t1t2|，∴（t1+t2）2＝5t1t2，

∴[4(a+1)]2＝5×8(a+1)，

解得a．