Question

【题目】已知函数（，）

（1）讨论的单调性；

（2）若对任意，恰有一个零点，求的取值范围.

Answer 1

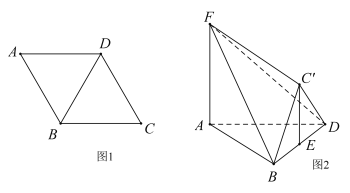
【答案】（1）见解析（2）

【解析】

（1）讨论的范围，得出的解的情况，从而得出的单调区间；
（2）分离参数可得，令，求出的单调性和值域，从而可得出的范围．

解法一：（1）依题意，，

令，，

①当时，，，在单调递增；

②当时，，由得，，

因为，所，设，，

则当时，，所以在单调递增；

当时，，所以在单调递减；

当时，，所以在单调递增；

综上，当时，在单调递增；

②当时，在单调递增，

在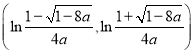单调递减，在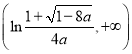单调递增.

（2）由得，，记，则，

（i）当时，由（1）知，在单调递增，

所以在单调递增，又因为，

当时，，时，

所以当时，对任意恰有一个零点.

（ii）当时，由（1）知，在单调递增，在单调递减，

在单调递增，其中，，

所以，在单调递增，在单调递减，在单调递增，

，所以，

所以极大

极小，

又因为当时，，时，

所以对任意，恰有一个零点，等价于恒成立或恒成立.

设，则，

当时，，所以在单调递增，

当时，，所以在单调递减，

又，，

因为，所以，所以，，

所以的值域为，的值域为，

即的值域为，的值域为，

所以，所以，

综上，的取值范围为.

解法二：（1）同解法一；

（2）（i）当时，由（1）知，在单调递增，

又因为，

所以取，则，取，则，

所以，所以在恰有一个零点，所以；

（ii）当时，由（1）知，在单调递增，在单调递减，

在单调递增，其中，，

，所以，

所以极大，

极小，

设，则，

当时，，所以在单调递增，+

当时，，所以在单调递减，

又，，

因为，所以，所以，，

①当时，，，

即，，所以当时，，

在不存在零点，

当时，取，则，

又因为，所以在恰有一个零点，所以恰有一个零点；.

②当时，因为，当时，，

所以，所以在恰有一个零点，

当时，，

所以，所以在恰有一个零点，

即，则，

则，

所以在单调递减，所以，

所以，即，

因为，，且在单调递减，

所以，即，所以，

所以，因为，，，

所以存在，满足，所以，，

所以