题目内容
【题目】已知曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ,直线
,直线![]() 的方程为
的方程为![]() ,且与曲线
,且与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设点![]() ,直线
,直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?若过定点,求该定点的坐标.
是否过定点?若过定点,求该定点的坐标.
【答案】(1)![]() ;(2)是,
;(2)是,![]() .
.
【解析】
(1)把已知等式根式里式子配方后由几何意义得出动点![]() 到两定点距离之和为定值,从而确定动点轨迹是椭圆,根据椭圆标准方程得出结论;
到两定点距离之和为定值,从而确定动点轨迹是椭圆,根据椭圆标准方程得出结论;
(2)设![]() 与
与![]() 的交点
的交点![]() ,
,![]() ,联立直线
,联立直线![]() 与曲线
与曲线![]() 的方程:
的方程: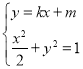 ,消
,消![]() 整理,应用韦达定理得
整理,应用韦达定理得![]() ,代入
,代入![]() ,得
,得![]() 的关系,由此求得直线
的关系,由此求得直线![]() 过定点的坐标.
过定点的坐标.
(1)由![]() 可化得
可化得
![]() ,设
,设![]() ,
,![]() ,
,
则等式即为![]() ,且
,且![]() ,所以曲线
,所以曲线![]() 是椭圆,焦点为
是椭圆,焦点为![]() ,
,![]() (在
(在
![]() 轴上),长半轴长
轴上),长半轴长![]() ,半焦距
,半焦距![]() ,短半轴长
,短半轴长![]() ,
,
所以曲线![]() 的方程为
的方程为![]() .
.
(2)联立直线![]() 与曲线
与曲线![]() 的方程:
的方程: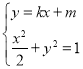 ,消
,消![]() 整理得
整理得
![]() ,
,
∵直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() ,
,
∴![]() ,得
,得![]() ,
,
设![]() 与
与![]() 的交点
的交点![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
由题意,![]()
![]()
∴![]()
![]()
![]() ,
,
由![]() 得
得![]() ,且满足
,且满足![]() ,则
,则![]() :
:![]() ,
,
所以直线![]() 经过定点
经过定点![]() .
.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目