题目内容
已知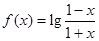 .
.
(1)求函数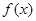 的定义域;
的定义域;
(2)判断并证明函数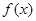 的奇偶性;
的奇偶性;
(3)若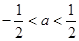 ,试比较
,试比较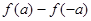 与
与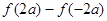 的大小.
的大小.
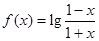 .
.(1)求函数
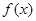 的定义域;
的定义域;(2)判断并证明函数
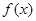 的奇偶性;
的奇偶性;(3)若
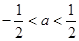 ,试比较
,试比较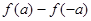 与
与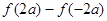 的大小.
的大小.(1)(-1,1)(2)奇函数(3)当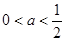 时,
时, 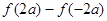 >
>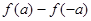 ;
;
当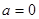 时,
时,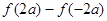 =
=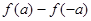 ;
;
当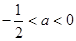 时,
时,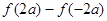 <
<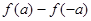
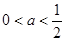 时,
时, 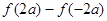 >
>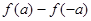 ;
;当
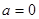 时,
时,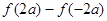 =
=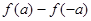 ;
;当
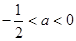 时,
时,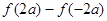 <
<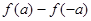
试题分析:解(1)函数
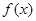 的定义域为(-1,1).
的定义域为(-1,1).(2)∵
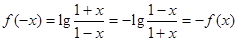 ,
,∴
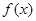 是奇函数.
是奇函数.(3)设
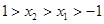 ,则
,则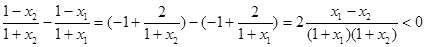 ,
,∴
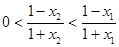 ,∴
,∴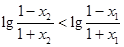 ,即
,即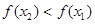 ,
,∴函数
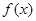 在(-1,1)上是减函数.
在(-1,1)上是减函数.由(2)知函数
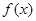 在(-1,1)上是奇函数,
在(-1,1)上是奇函数,∴
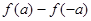 =
=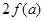 ,
,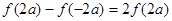 ,
,∴当
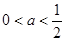 时,
时,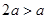 ,则
,则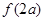 >
>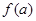 ,∴
,∴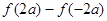 >
>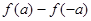 ;
;当
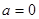 时,
时,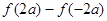 =
=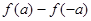 ;
;当
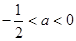 时,
时,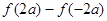 <
<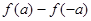 .
.点评:函数的单调性对求最值、判断函数值大小关系和证明不等式都有较大帮助。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域是
的定义域是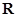 ,若对于任意的正数
,若对于任意的正数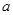 ,函数
,函数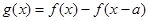 都是其定义域上的减函数,则函数
都是其定义域上的减函数,则函数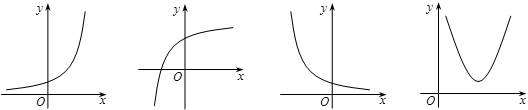
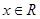 ,奇函数
,奇函数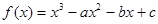 在
在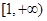 上单调,则实数b的取值范围是__________.
上单调,则实数b的取值范围是__________.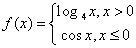 的图象上关于原点
的图象上关于原点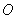 对称的点有 对.
对称的点有 对. 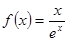 的一个单调递增区间是( )
的一个单调递增区间是( )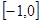

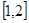
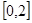
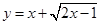 的值域是( )
的值域是( )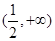
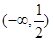
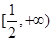
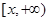
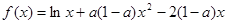 (
(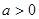 )
)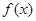 的定义域;(2)讨论函数
的定义域;(2)讨论函数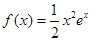 .
.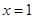 是函数
是函数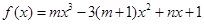 的一个极值点,其中
的一个极值点,其中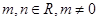
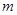 与
与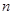 的关系式;
的关系式;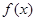 的单调区间;
的单调区间;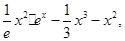
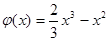 ;试比较g(x)与
;试比较g(x)与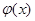 的大小。
的大小。