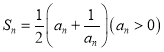题目内容
【题目】双曲线C的渐近线方程为
，一个焦点为F（0，﹣8），则该双曲线的标准方程为_____.已知点A（﹣6，0），若点P为C上一动点，且P点在x轴上方，当点P的位置变化时，△PAF的周长的最小值为_____.
【答案】
28
【解析】
答题空1：利用已知条件求出
，
，，然后求出双曲线方程即可
答题空2：利用双曲线的定义转化求解三角形的周长最小值即可
∵双曲线C的渐近线方程为
，一个焦点为F（0，﹣8），
∴
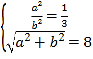，解得a=4，b=4
.
∴双曲线的标准方程为；
设双曲线的上焦点为F′（0，8），则|PF|=|PF′|+8，
△PAF的周长为|PF|+|PA|+|AF|=|PF′|+|PA|+|AF|+8.
当P点在第二象限，且A，P，F′共线时，|PF′|+|PA|最小，最小值为|AF′|=10.
而|AF|=10，故，△PAF的周长的最小值为10+10+8=28.
故答案为：；28.
练习册系列答案
一本好题口算题卡系列答案
相关题目
