Question

【题目】在直角坐标平面上的一列点，简记为．若由构成的数列满足，其中为方向与轴正方向相同的单位向量，则称为点列．

（1）判断，是否为点列，并说明理由；

（2）若为点列，且点在点的右上方．任取其中连续三点，判断的形状（锐角三角形、直角三角形、钝角三角形），并予以证明；

（3）若为点列，正整数，满足，求证：．

Answer 1

【答案】（1）是，理由详见解析；（2）钝角三角形，证明详见解析；（3）详见解析.

【解析】

(1)根据新定义表示出数列的通项公式，利用作差法比较的大小即可判断；

(2)由为点列得出的关系，利用两点间距离公式表示出三角形的各边长，可以分析得出最大角，结合余弦定理即可判断；

(3)利用累加的方法可以得出即可证明结论.

(1) 为点列.理由如下：

由题意可知，，所以，，即数列满足，所以为点列.

(2) 为钝角三角形.理由如下：

由题意可知，，所以，因为为点列，所以，又点在点的右上方，所以所以对其中连续三点，都有又 所以，所以为最大角，由余弦定理得，故为钝角，所以为钝角三角形.

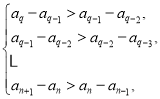(3)证明：由(2)知，因为为点列，所以.又正整数，满足，所以不妨设,则相加可得 同理可得，即又，所以.