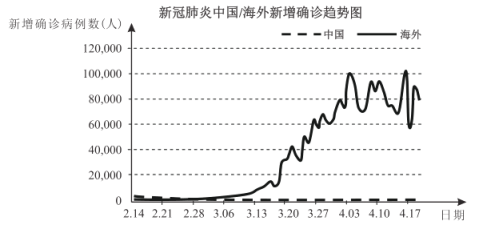
题目内容
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,边
,边![]() 上一点
上一点![]() ,这里
,这里![]() 异于
异于![]() .由
.由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足,再由
是垂足,再由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足,又由
是垂足,又由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足.同样的操作连续进行,得到点
是垂足.同样的操作连续进行,得到点![]() ,
,![]() ,
,![]() .设
.设![]() ,如图所示.
,如图所示.

(1)求![]() 的值;
的值;
(2)某同学对上述已知条件的研究发现如下结论:![]() ,问该同学这个结论是否正确并说明理由;
,问该同学这个结论是否正确并说明理由;
(3)用![]() 和
和![]() 表示
表示![]() .
.
【答案】(1)![]() (2)结论正确,证明见解析;(3)
(2)结论正确,证明见解析;(3)![]() ,
,![]() .
.
【解析】
(1)![]() ,根据向量数量积公式,求出
,根据向量数量积公式,求出![]() ,即可求解;
,即可求解;
(2)只需在![]() 中,求出
中,求出![]() ,判断
,判断![]() 是否成立即可,在
是否成立即可,在![]() 中,由余弦定理求出
中,由余弦定理求出![]() ,根据已知得出
,根据已知得出![]() ,进而求出
,进而求出![]() ,即可得到
,即可得到![]() ;
;
(3)由已知可得![]() ,
,![]() ,分别通过
,分别通过![]() ,
,![]() ,
,![]() ,将
,将![]() 用
用![]() 表示,结合
表示,结合![]() ,得到
,得到![]() 递推关系,进而求出
递推关系,进而求出![]() 的通项公式.
的通项公式.
(1)∵![]() ,
,
∴![]() .
.
∴![]() .
.
(2)该同学的结论正确,证明如下:
由(1)及已知,得![]() ,
,![]() ,
,![]() .
.
由余弦定理知![]() .
.
又![]() ,则
,则![]() .
.
∴![]() .
.
即![]() .
.
(3)由已知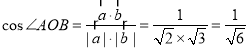 .
.
∵![]() ,∴
,∴![]() .
.
∴![]()
![]()
![]()
![]()
![]() .
.
即![]() ,也即
,也即![]() .
.
∴![]() ,
,![]() ,
,
![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列,
的等比数列,
![]() ,
,
∴![]() ,
,![]() .
.

练习册系列答案
相关题目