��Ŀ����
����Ŀ��С��ÿ��ӼҲ���ȥѧУ��������·�߿���ѡ��һ��·�ߣ��������ţ����õȺ�ƣ�ƽ����ʱ910�룻�ڶ���·�ߣ�Ҫ�����������̵�·�ڣ���ͼ��A��ΪС���ң�D��ΪѧУ����·��![]() ��240�룬��B����һ���̵ƣ����ʱ��120�룬�̵�ʱ��30�룬��·��
��240�룬��B����һ���̵ƣ����ʱ��120�룬�̵�ʱ��30�룬��·��![]() ��450�룬��C��Ҳ��һ���̵ƣ����ʱ��100�룬�̵�ʱ��50�룬��·��
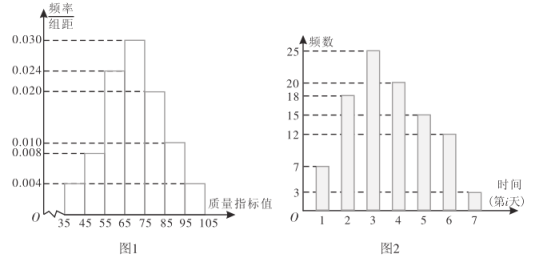
��450�룬��C��Ҳ��һ���̵ƣ����ʱ��100�룬�̵�ʱ��50�룬��·��![]() ��200��.С��������60������飬ÿ�춼ѡ��ڶ���·�ߣ�����¼����B���ȴ���Ƶ�ʱ������ͳ�ƣ�60������48����B��������ƣ����ݼ�¼��48��ȴ����ʱ�������ݻ����������Ƶ�ʷֲ�ֱ��ͼ.��֪B����C���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ���Һ��̵�֮���л���ʱ����.
��200��.С��������60������飬ÿ�춼ѡ��ڶ���·�ߣ�����¼����B���ȴ���Ƶ�ʱ������ͳ�ƣ�60������48����B��������ƣ����ݼ�¼��48��ȴ����ʱ�������ݻ����������Ƶ�ʷֲ�ֱ��ͼ.��֪B����C���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ���Һ��̵�֮���л���ʱ����.

��1����С��ѡ��ڶ���·�ߣ��赱С������B����ʱ��ΪB����������ĵ�x�루![]() ��ʱ��С����B���ȴ���Ƶ�ʱ��Ϊy�룬��y����x�ĺ����Ľ���ʽ��
��ʱ��С����B���ȴ���Ƶ�ʱ��Ϊy�룬��y����x�ĺ����Ľ���ʽ��
��2����С��ѡ��ڶ���·�ߣ������С����B��������Ƶĸ��ʣ�����С���Ƿ������B����C����������ƣ�
��3����ȡ�����е���Ϊ�������Ӧ�ĵȴ���Ƶ�ʱ������������·�ߵ�ƽ����ʱ��Ϊ�������ݣ�С��Ӧѡ����һ��·�ߣ�
���𰸡���1��![]() ����2������С����
����2������С����![]() ��������Ƶĸ���Ϊ
��������Ƶĸ���Ϊ![]() ��С����������
������������![]() ����
����![]() ����������ƣ���3��С��Ӧ��ѡ���һ��·��.
����������ƣ���3��С��Ӧ��ѡ���һ��·��.
��������
��1���ֱ���![]() ��
��![]() ��������µõ��ȴ����ʱ���������õ������
��������µõ��ȴ����ʱ���������õ������
��2�����ݼ��θ����ʹ�ʽ����ɵ�������ʣ������������̵Ƶ���ʱ����Ϊ![]() ��ʱ����
��ʱ����![]() �����жϳ�����ͬʱ������ƣ�
�����жϳ�����ͬʱ������ƣ�
��3������Ƶ�ʷֲ�ֱ��ͼ����ɵõȴ���Ƶ�ƽ��ʱ��������ȷ���ڶ���·�ߵ�ƽ��ʱ�����Ӷ�ȷ�����.
��1����![]() ʱ��С���ȴ����ʱ��
ʱ��С���ȴ����ʱ��![]() ��
��
��![]() ʱ��С������ȴ�����
ʱ��С������ȴ�����![]() ��
��
����������![]() .
.
��2������С����![]() ��������Ƶĸ���
��������Ƶĸ���![]() .
.
��ΪС����![]() ����ʱ��һ����
����ʱ��һ����![]() ���������
���������![]() ���
���![]() ��
��![]() ���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ����
���ĺ�������ʱ��ǡ��ʼ�ձ�����ͬ����![]() ����
����![]() �����̵Ƶ�ʱ������ȣ�������С����·��
�����̵Ƶ�ʱ������ȣ�������С����·��![]() �����ʱ��
�����ʱ��![]() ���
���![]() ������������
������С������![]() ����ʱ��һ����
����ʱ��һ����![]() ���������
���������![]() ��֮������С��������
��֮������С��������![]() ��������ƣ����С����������
��������ƣ����С����������![]() ����
����![]() �����������.
�����������.
��3��С���ߵڶ���·��ƽ���ȴ���Ƶ�ʱ��Ϊ��
![]()
![]() ���룩��
���룩��
С���ߵڶ���·��ƽ����ʱΪ��![]() ���룩��
���룩��
![]() ��
��![]() С��Ӧ��ѡ���һ��·��.
С��Ӧ��ѡ���һ��·��.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�