题目内容
【题目】根据下列关系式,算出数列的前4项,然后猜想它的通项,并用数学归纳法证明你的猜想.
(1)![]() ;
;
(2)![]() ;
;
(3)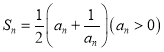 .
.
【答案】(1)![]() ,
,![]() ,证明见解析; (2)
,证明见解析; (2)![]() ,
,![]() ,证明见解析; (3)
,证明见解析; (3)![]() ,
,![]() ,证明见解析.
,证明见解析.
【解析】
分别求出数列的前几项,猜测数列的通项公式,利用数学归纳法,作出证明即可.
(1)由![]() ,
,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ,
,
由此可猜测数列的通项公式为:![]() ,
,
证明如下:
①当![]() 时,
时,![]() ,显然成立;
,显然成立;
②假设![]() 时,结论成立,即
时,结论成立,即![]() ,
,
则当![]() 时,
时,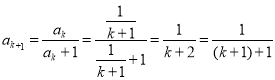 ,
,
即当![]() 时也成立,
时也成立,
由①②可得![]() 对
对![]() 都成,即
都成,即![]() ,
,![]() .
.
(2)由![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() ;
;
猜测数列的通项公式为:![]() ,
,
证明如下:
①当![]() 时,
时,![]() ,显然成立;
,显然成立;
②假设![]() 时,结论成立,即
时,结论成立,即![]() ,
,
则当![]() 时,
时,![]() ,且
,且![]() ,
,
两式相减可得![]() ,即
,即![]() ,
,
整理得![]() ,
,
即当![]() 时也成立,
时也成立,
由①②可得![]() 对
对![]() 都成,即
都成,即![]() ,
,![]() .
.
(3)由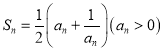 ,
,
令![]() ,可得
,可得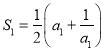 ,即
,即 ,因为
,因为![]() ,则
,则![]() ;
;
令![]() ,可得
,可得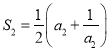 ,即
,即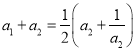 ,解得
,解得![]() ;
;
令![]() ,可得
,可得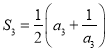 ,即
,即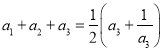 ,解得
,解得![]() ;
;
令![]() ,可得
,可得 ,即
,即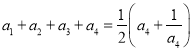 ,解得
,解得![]() ;
;
猜测数列的通项公式为:![]() .
.
证明如下:
①当![]() 时,
时,![]() ,命题成立;
,命题成立;
②假设![]() 时,结论成立,即
时,结论成立,即![]() ,
,
则当![]() 时,
时,![]()
![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即当![]() 时也成立,
时也成立,
由①②可得![]() 对
对![]() 都成,即
都成,即![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目