题目内容
【题目】某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度![]() (单位:毫克/立方米)随着时间
(单位:毫克/立方米)随着时间![]() (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
(1)若一次喷洒1个单位的去污剂,则去污时间可达几天?
(2)若第一次喷洒1个单位的去污剂,6天后再喷洒![]() 个单位的去污剂,要使接下来的4天中能够持续有效去污,试求
个单位的去污剂,要使接下来的4天中能够持续有效去污,试求![]() 的最小值?(精确到
的最小值?(精确到![]() )
)
【答案】(1)7;(2)![]() .
.
【解析】
(1)依题意,令![]() ,分段解不等式即可得解;
,分段解不等式即可得解;
(2)设从第一次喷洒起,经![]() 天空气中的去污剂浓度为
天空气中的去污剂浓度为![]() ,得
,得![]() ,依题意
,依题意![]() 对一切
对一切![]() 恒成立,只需
恒成立,只需![]() 即可.
即可.
(1)依题意,令![]() 则
则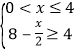 或
或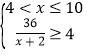
解得 ![]() 或
或![]()
![]()
![]() .
.
![]() 一次喷洒1个单位的去污剂,去污时间可达7天.
一次喷洒1个单位的去污剂,去污时间可达7天.
(2)设从第一次喷洒起,经![]() 天空气中的去污剂浓度为
天空气中的去污剂浓度为![]() ,
,
则![]() ,
,
依题意![]() 对一切
对一切![]() 恒成立
恒成立 ![]()
![]() ,
,
又![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
![]()
![]() ,故
,故![]() 的最小值为0.2.
的最小值为0.2.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目


