题目内容
【题目】如图,三棱柱![]() 的所有棱长都是2,
的所有棱长都是2,![]() 平面ABC,D,E分别是AC,
平面ABC,D,E分别是AC,![]() 的中点.
的中点.
![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据线面垂直和面面垂直判定和性质,证得![]() ,通过三角形全等,证得
,通过三角形全等,证得![]() ,再根据线面垂直的判定定理,证得
,再根据线面垂直的判定定理,证得![]() 平面
平面![]() ;
;
(2) 建立空间直角坐标系,向量法求二面角的余弦值.
(1)∵![]() ,D是AC的中点,∴
,D是AC的中点,∴![]() ,
,
∵![]() 平面ABC,∴平面
平面ABC,∴平面![]() 平面ABC,
平面ABC,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵在正方形![]() 中,D,E分别是AC,
中,D,E分别是AC,![]() 的中点,易证得∴△A1AD≌△ACE
的中点,易证得∴△A1AD≌△ACE
∴∠A1DA=∠AEC, ∵∠AEC+∠CAE=90°,∴∠A1DA+∠CAE=90° ,即![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
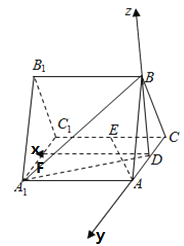
(3)取![]() 中点F,以DF,DA,DB为x,y,z轴建立空间直角坐标系,
中点F,以DF,DA,DB为x,y,z轴建立空间直角坐标系,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面DBE的一个法向量为![]() ,则
,则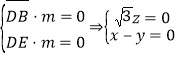 ,
,
令![]() ,则
,则![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则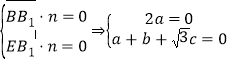 ,
,
令![]() ,则
,则![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,观察可知
,观察可知![]() 为钝角,
为钝角,
![]() ,
,
∴![]() ,故二面角
,故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)










