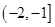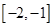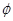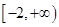题目内容
设f(x)为定义在R上的奇函数,当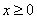 时,
时,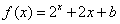 (
(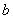 为常数),则
为常数),则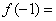 ( )
( )
| A.3 | B.1 | C.-1 | D.-3 |
D
解析试题分析:根据f(x)为定义在R上的奇函数则f(0)=0求出b的值,然后根据奇函数得到f(-2)=-f(2)代入解析式可求出所求.解:∵f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),f(0)=1+b=0,b=-1.∴f(-1)=-f(1)=-(21+2+(-1))=-3.故答案为:D
考点:函数奇偶性
点评:本题主要考查了函数奇偶性的性质,以及函数求值,属于基础题.

练习册系列答案
相关题目
若函数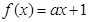 在R上递减,则函数
在R上递减,则函数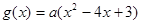 的增区间是 ( )
的增区间是 ( )
| A.(2,+∞) | B.(-∞,2) | C.(-2,+∞) | D.(-∞,-2) |
若偶函数f(x)在区间(-∞,-1]上是增函数,则( )
A.f(-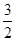 )<f(-1)<f(2) )<f(-1)<f(2) | B.f(-1)<f(-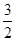 )<f(2) )<f(2) |
C.f(2)<f(-1)<f(-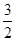 ) ) | D.f(2)<f(-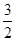 )<f(-1) )<f(-1) |
已知函数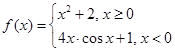 ,且方程
,且方程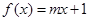 在区间
在区间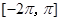 内有两个不等的实根,则实数
内有两个不等的实根,则实数 的取值范围( )
的取值范围( )
A.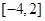 | B.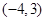 | C.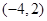 | D.[2,4] |
函数f(x)=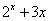 的零点所在的一个区间是
的零点所在的一个区间是
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2) |
下列函数中,与函数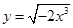 相同的是( )
相同的是( )
A.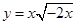 | B.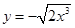 |
C.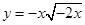 | D.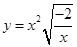 |
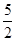 )=( )
)=( )
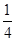
 上的函数
上的函数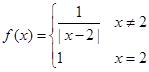 ,若关于
,若关于 的方程
的方程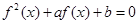 有3个不同实数解
有3个不同实数解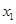 、
、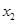 、
、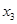 ,且
,且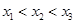 ,则下列说法中错误的是( )
,则下列说法中错误的是( )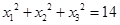
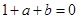
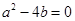
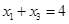
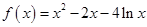 ,不等式
,不等式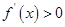 的解集为
的解集为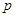 ,关于
,关于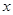 的不等式
的不等式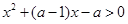 的解集记为
的解集记为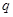 ,已知
,已知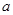 的取值范围是( )
的取值范围是( )