题目内容
函数f(x)=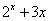 的零点所在的一个区间是
的零点所在的一个区间是
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2) |
B
解析试题分析:解:∵函数f(x)=2x+3x是R上的连续函数,且单调递增,f(-1)=2-1+3×(-1)=-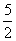 <0,f(0)=20+0=1>0,∴f(-1)f(0)<0.∴f(x)=2x+3x的零点所在的一个区间为(-1,0),故答案为 (-1,0).选B.
<0,f(0)=20+0=1>0,∴f(-1)f(0)<0.∴f(x)=2x+3x的零点所在的一个区间为(-1,0),故答案为 (-1,0).选B.
考点:函数零点
点评:本题主要考查函数零点的概念与零点定理的应用,属于容易题。

练习册系列答案
相关题目
若函数 的导函数
的导函数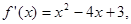 则函数
则函数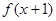 的单调递减区间是( )
的单调递减区间是( )
| A.(2,4) | B.(-3,-1) | C.(1,3) | D.(0,2) |
设f(x)为定义在R上的奇函数,当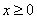 时,
时,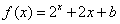 (
(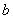 为常数),则
为常数),则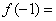 ( )
( )
| A.3 | B.1 | C.-1 | D.-3 |
已知函数 的定义域为
的定义域为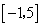 ,部分对应值如下表:
,部分对应值如下表:
 的导函数
的导函数 的图象如图所示,
的图象如图所示,
则下列关于函数 的命题:
的命题:
① 函数 是周期函数;
是周期函数;
② 函数 在
在 是减函数;
是减函数;
③ 如果当 时,
时, 的最大值是2,那么
的最大值是2,那么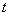 的最大值为4;
的最大值为4;
④ 当 时,函数
时,函数 有4个零点。
有4个零点。
其中真命题的个数是 ( )
| A.4个 | B.3个 | C.2个 | D.1个 |
如图是函数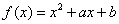 的部分图象,则函数
的部分图象,则函数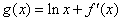 的零点所在的区间是( )
的零点所在的区间是( )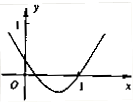
A. | B.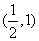 | C.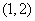 | D.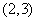 |
设f(x)为周期是2的奇函数,当 时,f(x)=x(x+1),则当
时,f(x)=x(x+1),则当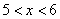 时,f(x)的表达式为
时,f(x)的表达式为
| A.(x-5)(x-4) | B.(x-6)(x-5) | C.(x-6)(5-x) | D.(x-6)(7-x) |
函数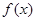 对任意自然数
对任意自然数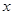 ,满足
,满足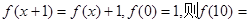 ( )
( )
| A.11 | B.12 | C.13 | D.14 |
若 ,则( )
,则( )
A.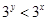 | B.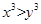 | C. | D.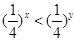 |
已知函数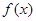 的导函数为
的导函数为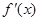 ,且满足
,且满足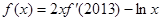 ,则
,则 ( )
( )
A.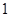 | B. | C. | D.无法确定 |