题目内容
已知圆C: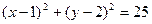 ,直线
,直线 :
: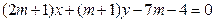
(1)求证:直线 过定点;
过定点;
(2)判断该定点与圆的位置关系;
(3)当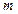 为何值时,直线
为何值时,直线 被圆C截得的弦最长。
被圆C截得的弦最长。
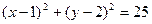 ,直线
,直线 :
: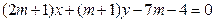
(1)求证:直线
 过定点;
过定点;(2)判断该定点与圆的位置关系;
(3)当
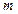 为何值时,直线
为何值时,直线 被圆C截得的弦最长。
被圆C截得的弦最长。(1)证明见解析
(2)点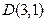 在圆C内;
在圆C内;
(3)当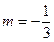 时,直线
时,直线 被圆C截得的弦最长.
被圆C截得的弦最长.
(2)点
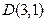 在圆C内;
在圆C内;(3)当
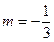 时,直线
时,直线 被圆C截得的弦最长.
被圆C截得的弦最长.(1)证明:把直线 的方程整理成
的方程整理成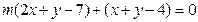 ,
,
由于 的任意性,有
的任意性,有 ,解此方程组,得
,解此方程组,得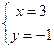 ,
,
所以直线 恒过定点
恒过定点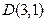 ;
;
(2)把点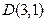 的坐标代入圆C的方程,得左边
的坐标代入圆C的方程,得左边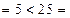 右边,
右边,
∴点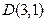 在圆C内;
在圆C内;
(3)当直线 经过圆心C(1,2)时,被截得的弦最长(等于圆的直径长),
经过圆心C(1,2)时,被截得的弦最长(等于圆的直径长),
此时,直线 的斜率
的斜率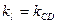 ,
,
由直线 的方程得
的方程得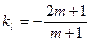 ,由点C、D的坐标得
,由点C、D的坐标得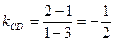
∴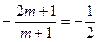 ,解得
,解得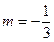 ,
,
所以,当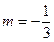 时,直线
时,直线 被圆C截得的弦最长.
被圆C截得的弦最长.
 的方程整理成
的方程整理成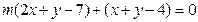 ,
,由于
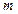 的任意性,有
的任意性,有 ,解此方程组,得
,解此方程组,得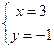 ,
,所以直线
 恒过定点
恒过定点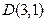 ;
;(2)把点
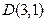 的坐标代入圆C的方程,得左边
的坐标代入圆C的方程,得左边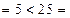 右边,
右边,∴点
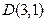 在圆C内;
在圆C内;(3)当直线
 经过圆心C(1,2)时,被截得的弦最长(等于圆的直径长),
经过圆心C(1,2)时,被截得的弦最长(等于圆的直径长),此时,直线
 的斜率
的斜率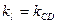 ,
,由直线
 的方程得
的方程得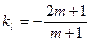 ,由点C、D的坐标得
,由点C、D的坐标得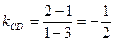
∴
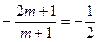 ,解得
,解得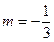 ,
,所以,当
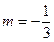 时,直线
时,直线 被圆C截得的弦最长.
被圆C截得的弦最长.
练习册系列答案
相关题目
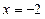 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线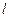 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为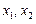 .①求证:
.①求证: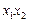 为定值;②试用
为定值;②试用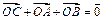 ,且
,且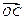 =
= a.
a.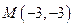 的直线
的直线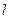 被圆
被圆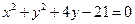 所截得的弦长为
所截得的弦长为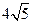 ,
,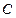 的圆心在直线
的圆心在直线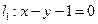 上,圆
上,圆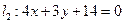 相切,
相切,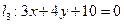 所得弦长为
所得弦长为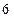 ,求圆
,求圆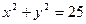 截直线
截直线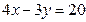 所得弦的垂直平分线方程是( ).
所得弦的垂直平分线方程是( ).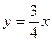
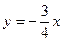
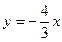
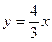
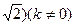 与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。