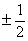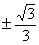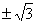题目内容
自点P(-6,7)发出的光线l射到x轴上点A处,被x轴反射,其反射光线所在直线与圆x2+y2-8x-6y+21=0相切于点Q.求光线l所在直线方程.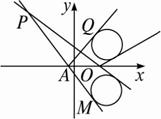 
l所在直线的方程为3x+4y-10=0或4x+3y+3=0.?
如图,作圆x2+y2-8x-6y+21=0关于x轴的对称圆x2+y2-8x+6y+21=0,?
由几何光学原理，知
直线l与圆x2+y2-8x+6y+21=0相切,?
又∵l的斜率必存在,故可设直线l:y-7=k(x+6),
即kx-y+6k+7=0.
由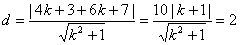
,得
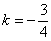或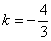
,
故光线l所在直线的方程为3x+4y-10=0或4x+3y+3=0.?
由几何光学原理，知
直线l与圆x2+y2-8x+6y+21=0相切,?
又∵l的斜率必存在,故可设直线l:y-7=k(x+6),
即kx-y+6k+7=0.
由
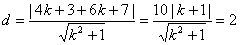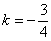,得或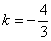,故光线l所在直线的方程为3x+4y-10=0或4x+3y+3=0.?
练习册系列答案
阅读快车系列答案
相关题目
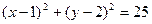，直线
:
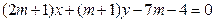
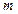为何值时，直线
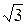x+y－2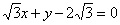
截圆x2+y2=4所得劣弧所对的圆心角为( ) 
