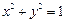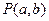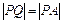题目内容
将圆x2 + y2 + 2x – 2y = 0按向量a= (1,–1)平移得到圆O,直线l和圆O相交于A、B两点,若在圆O上存在点C,使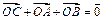 ,且
,且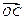 =
= a.
a.
(1)求 的值;(2)求弦AB的长;(3)求直线l的方程.
的值;(2)求弦AB的长;(3)求直线l的方程.
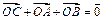 ,且
,且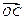 =
= a.
a.(1)求
 的值;(2)求弦AB的长;(3)求直线l的方程.
的值;(2)求弦AB的长;(3)求直线l的方程.(1) =±1.(2)AB =
=±1.(2)AB =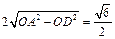 (3)直线AB的斜率kAB = 1.AB的方程为x – y +1 = 0.当
(3)直线AB的斜率kAB = 1.AB的方程为x – y +1 = 0.当 = –1时,AB的方程为x – y -1 = 0.
= –1时,AB的方程为x – y -1 = 0.
 =±1.(2)AB =
=±1.(2)AB =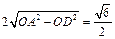 (3)直线AB的斜率kAB = 1.AB的方程为x – y +1 = 0.当
(3)直线AB的斜率kAB = 1.AB的方程为x – y +1 = 0.当 = –1时,AB的方程为x – y -1 = 0.
= –1时,AB的方程为x – y -1 = 0.1)圆x2 + y2 + 2x – 2y = 0按向量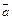 = (1,–1)平移,得到圆O:x2 + y2 = 2,所以半径r =
= (1,–1)平移,得到圆O:x2 + y2 = 2,所以半径r =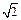 .∵|
.∵|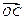 | = |
| = | a | =
a | =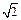 ,即|
,即| || a | =
|| a | =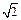 ,∴
,∴ =±1.
=±1.
(2)取AB中点D,连结OD,∵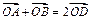 ,由
,由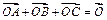 可得
可得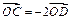 ,
,
∴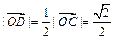 ,又∵OD⊥AB,∴AB =
,又∵OD⊥AB,∴AB =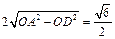 .
.
(3)当 =1时,
=1时,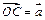 = (1,–1),设D点坐标为(x,y),则
= (1,–1),设D点坐标为(x,y),则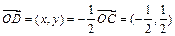 ,又∵直线AB的斜率kAB = –
,又∵直线AB的斜率kAB = – = 1.AB的方程为x – y +1 = 0.
= 1.AB的方程为x – y +1 = 0.
同理当 = –1时,AB的方程为x – y -1 = 0.
= –1时,AB的方程为x – y -1 = 0.
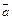 = (1,–1)平移,得到圆O:x2 + y2 = 2,所以半径r =
= (1,–1)平移,得到圆O:x2 + y2 = 2,所以半径r =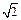 .∵|
.∵|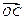 | = |
| = | a | =
a | =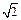 ,即|
,即| || a | =
|| a | =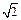 ,∴
,∴ =±1.
=±1.(2)取AB中点D,连结OD,∵
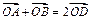 ,由
,由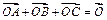 可得
可得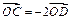 ,
,∴
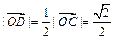 ,又∵OD⊥AB,∴AB =
,又∵OD⊥AB,∴AB =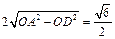 .
.(3)当
 =1时,
=1时,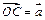 = (1,–1),设D点坐标为(x,y),则
= (1,–1),设D点坐标为(x,y),则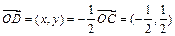 ,又∵直线AB的斜率kAB = –
,又∵直线AB的斜率kAB = – = 1.AB的方程为x – y +1 = 0.
= 1.AB的方程为x – y +1 = 0.同理当
 = –1时,AB的方程为x – y -1 = 0.
= –1时,AB的方程为x – y -1 = 0.
练习册系列答案
相关题目
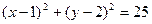 ,直线
,直线 :
: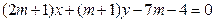
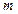 为何值时,直线
为何值时,直线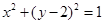 相切,且在每坐标轴上截距相等的距离有( )
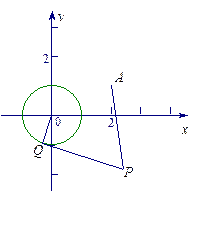
相切,且在每坐标轴上截距相等的距离有( )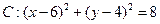 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
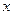 轴上,椭圆C上的点到焦点的最大值为
轴上,椭圆C上的点到焦点的最大值为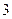 ,最小值为
,最小值为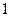 .
.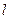 :
: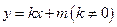 与椭圆交于不同的两点
与椭圆交于不同的两点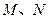 (
(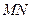 为直径的圆经过椭圆的右顶点
为直径的圆经过椭圆的右顶点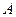 .求证:直线
.求证:直线