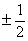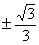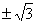题目内容
已知过点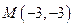 的直线
的直线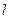 被圆
被圆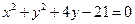 所截得的弦长为
所截得的弦长为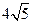 ,
,
求直线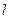 的方程.
的方程.
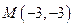 的直线
的直线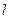 被圆
被圆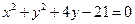 所截得的弦长为
所截得的弦长为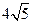 ,
,求直线
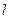 的方程.
的方程.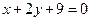 ,或
,或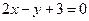
将圆的方程写成标准形式,得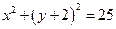 ,所以,圆心的坐标是
,所以,圆心的坐标是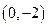 ,半径长
,半径长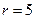 .
.
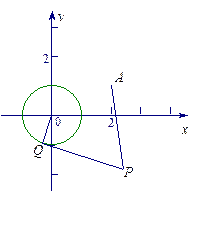
如图,因为直线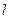 被圆所截得的弦长是
被圆所截得的弦长是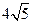 ,所以弦心距为
,所以弦心距为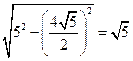 ,
,
即圆心到所求直线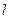 的距离为
的距离为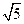 .
.
因为直线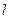 过点
过点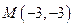 ,所以可设所求直线
,所以可设所求直线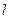 的方程为
的方程为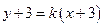 ,即
,即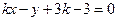 .
.
根据点到直线的距离公式,得到圆心到直线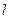 的距离
的距离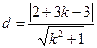 .
.
因此,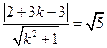 ,即
,即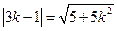 ,
,
两边平方,并整理得到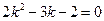 ,
,
解得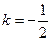 ,
,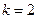 .
.
所以,所求直线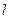 有两条,它们的方程分别为
有两条,它们的方程分别为
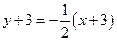 ,或
,或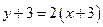 .
.
即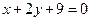 ,或
,或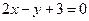 .
.
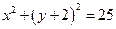 ,所以,圆心的坐标是
,所以,圆心的坐标是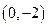 ,半径长
,半径长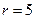 .
.如图,因为直线
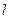 被圆所截得的弦长是
被圆所截得的弦长是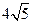 ,所以弦心距为
,所以弦心距为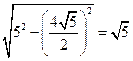 ,
,即圆心到所求直线
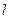 的距离为
的距离为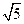 .
.因为直线
 过点
过点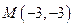 ,所以可设所求直线
,所以可设所求直线 的方程为
的方程为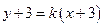 ,即
,即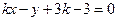 .
.根据点到直线的距离公式,得到圆心到直线
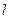 的距离
的距离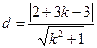 .
.因此,
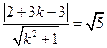 ,即
,即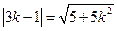 ,
,两边平方,并整理得到
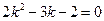 ,
,解得
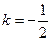 ,
,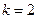 .
.所以,所求直线
 有两条,它们的方程分别为
有两条,它们的方程分别为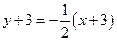 ,或
,或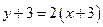 .
.即
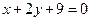 ,或
,或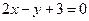 .
.
练习册系列答案
相关题目
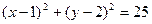 ,直线
,直线 :
: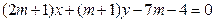
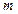 为何值时,直线
为何值时,直线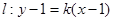 和圆
和圆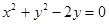 的位置关系是 ( )
的位置关系是 ( )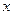 轴上,椭圆C上的点到焦点的最大值为
轴上,椭圆C上的点到焦点的最大值为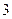 ,最小值为
,最小值为 .
.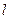 :
: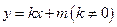 与椭圆交于不同的两点
与椭圆交于不同的两点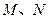 (
(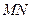 为直径的圆经过椭圆的右顶点
为直径的圆经过椭圆的右顶点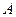 .求证:直线
.求证:直线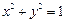
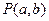
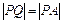
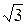 x+y-2
x+y-2