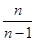题目内容
(本小题满分12分)已知函数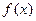 =
=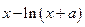 在
在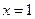 处取得极值.
处取得极值.
(1)求实数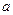 的值;
的值;
(2) 若关于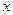 的方程
的方程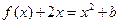 在
在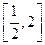 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数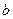 的取值范围;
的取值范围;
(3) 证明: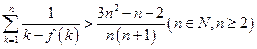 .参考数据:
.参考数据: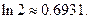
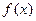 =
=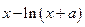 在
在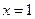 处取得极值.
处取得极值.(1)求实数
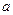 的值;
的值;(2) 若关于
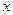 的方程
的方程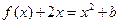 在
在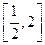 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数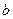 的取值范围;
的取值范围;(3) 证明:
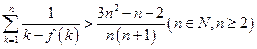 .参考数据:
.参考数据: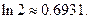
解(1)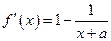 ,由题意得,
,由题意得,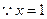 是
是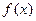 的一个极值点,
的一个极值点,
∴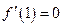 ,即
,即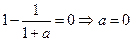 …… ………1分
…… ………1分
(2) 由(1)得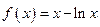 ,∴
,∴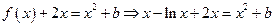
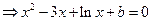
设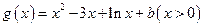 ,
,
则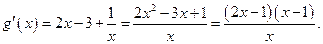
当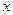 变化时,
变化时,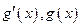 的变化情况如下表:
的变化情况如下表:
当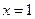 时,
时,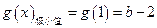 ,
,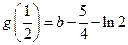 ,
,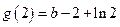
∵方程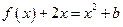 在
在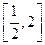 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
∴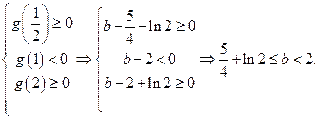
(3)∵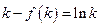 ,
,
∴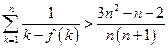
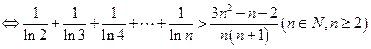
设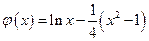 ,则
,则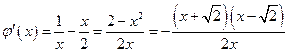
当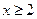 时,
时,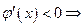 函数
函数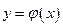 在
在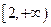 上是减函数,
上是减函数,
∴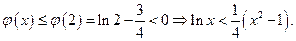
∴当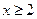 时,
时,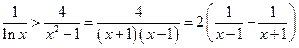 ,
,
∴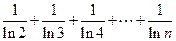
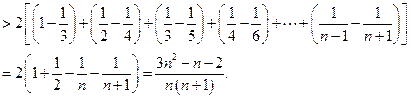
∴原不等式成立.
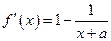 ,由题意得,
,由题意得,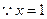 是
是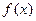 的一个极值点,
的一个极值点,∴
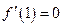 ,即
,即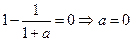 …… ………1分
…… ………1分(2) 由(1)得
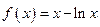 ,∴
,∴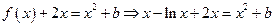
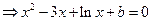
设
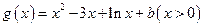 ,
,则
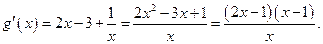
当
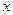 变化时,
变化时,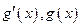 的变化情况如下表:
的变化情况如下表: | 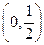 | 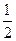 | 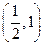 | 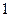 | 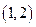 | 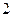 |
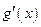 | 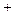 | 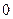 | 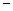 | 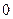 | 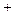 | |
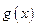 | 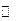 | 极大值 | 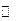 | 极小值 | 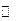 | 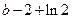 |
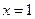 时,
时,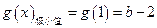 ,
,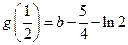 ,
,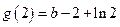
∵方程
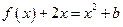 在
在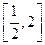 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,∴
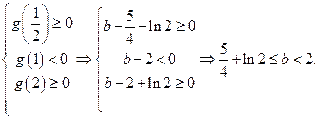
(3)∵
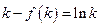 ,
,∴
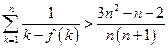
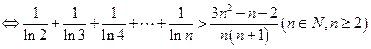
设
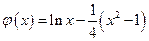 ,则
,则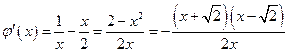
当
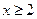 时,
时,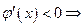 函数
函数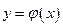 在
在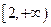 上是减函数,
上是减函数,∴
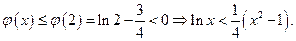
∴当
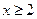 时,
时,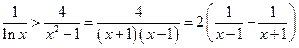 ,
,∴
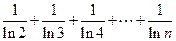
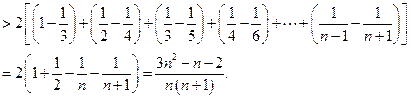
∴原不等式成立.
略

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
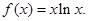 (I)求函数
(I)求函数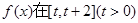 上的最小值;(II)求证:对一切
上的最小值;(II)求证:对一切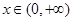 ,都有
,都有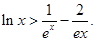
 设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.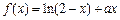 在(0,1)内是增函数.
在(0,1)内是增函数.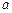 的取值范围;
的取值范围;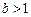 ,求证:
,求证: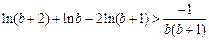 .
. 过点
过点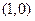 ,且与曲线
,且与曲线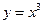 和
和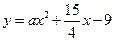 都相切,
都相切,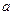 的值。
的值。
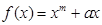 的导函数为
的导函数为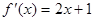 ,则数列
,则数列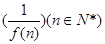 的前
的前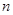 项
项