题目内容
(本题13分)
已知f(x)=lnx+x2-bx.
(1)若函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当b=-1时, 设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
已知f(x)=lnx+x2-bx.
(1)若函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当b=-1时,
 设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.解:(1)∵f(x)在(0,+∞)上递增,
∴f ′(x)=+2x-b≥0,对x∈(0,+∞)恒成立,
即b≤+2x对x∈(0,+∞)恒成立,
∴只 需b≤min
需b≤min  (x>0),
(x>0),
∵x>0,∴+2x≥2,当且仅当x=时取“=”,
∴b≤2,
∴b的取值范围为(-∞,2].
(2)当b=-1时,g(x)=f(x)-2x2=lnx-x2+x,其定义域是(0,+∞),
∴g′(x)=-2x+1
=-=-,
令g′(x)=0,即-=0,
∵x>0,∴x=1,
当0<x<1时,g′(x)>0;当x>1时,g′ (x)<0,
(x)<0,
∴函数g(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴当x≠1时,g(x)<g(1),即g(x)<0,当x=1时,g(x)=0.
∴函数g(x)只有一个零点.
∴f ′(x)=+2x-b≥0,对x∈(0,+∞)恒成立,
即b≤+2x对x∈(0,+∞)恒成立,
∴只
 需b≤min
需b≤min  (x>0),
(x>0),∵x>0,∴+2x≥2,当且仅当x=时取“=”,
∴b≤2,
∴b的取值范围为(-∞,2].
(2)当b=-1时,g(x)=f(x)-2x2=lnx-x2+x,其定义域是(0,+∞),
∴g′(x)=-2x+1
=-=-,
令g′(x)=0,即-=0,
∵x>0,∴x=1,
当0<x<1时,g′(x)>0;当x>1时,g′
 (x)<0,
(x)<0,∴函数g(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴当x≠1时,g(x)<g(1),即g(x)<0,当x=1时,g(x)=0.
∴函数g(x)只有一个零点.
略

练习册系列答案
相关题目
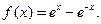
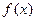 的导数
的导数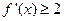 ;
;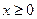 都有
都有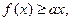 求a的取值范围。
求a的取值范围。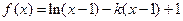 ,
,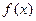 的单调区间;
的单调区间;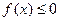 恒成立,试确定实数
恒成立,试确定实数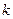 的取
的取 值范围;
值范围;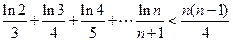 (
(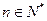 且
且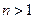 )
) x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0. )求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
)求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.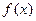 =
=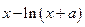 在
在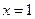 处取得极值.
处取得极值.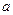 的值;
的值;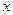 的方程
的方程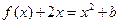 在
在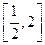 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数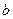 的取值范围;
的取值范围;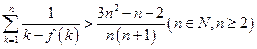 .参考数据:
.参考数据: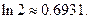
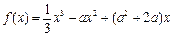 ,
,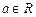 .
.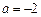 时,求
时,求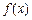 在闭区间
在闭区间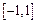 上的最大值与最小值;
上的最大值与最小值;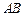 :
: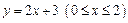 与导函数
与导函数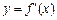 的图像只有一个交点,且交点在线段
的图像只有一个交点,且交点在线段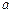 的取值范围.
的取值范围.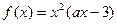 ,其中a为常数.
,其中a为常数.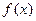 的一个极值点,求a的值;
的一个极值点,求a的值;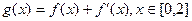 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.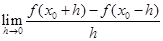 =( )
=( )