Question

【题目】已知圆O：x2+y2＝3，直线PA与圆O相切于点A，直线PB垂直y轴于点B，且|PB|＝2|PA|.

（1）求点P的轨迹E的方程；

（2）过点（1，0）且与x轴不重合的直线与轨迹E相交于P，Q两点，在x轴上是否存在定点D，使得x轴是∠PDQ的角平分线，若存在，求出D点坐标，若不存在，说明理由.

Answer 1

【答案】（1）（2）存在；定点D（4，0）

【解析】

（1）设P（x，y），根据直线PA与圆O相切于点A，利用切线长公式得到|PA|2＝x2+y2﹣3，|再根据直线PB垂直y轴于点B，得到|PB|2＝x2，然后由|PB|＝2|PA|求解.

（2）设直线l的方程为：x＝my+1，与椭圆方程联立，利用韦达定理得到，，代入kPD+kQD＝0，化简整理得，解得x0即可.

（1）设P（x，y），因为直线PA与圆O相切于点A，

所以|PA|2＝|PO|2﹣3＝x2+y2﹣3，|

又因为直线PB垂直y轴于点B，

所以|PB|2＝x2，

又因为|PB|＝2|PA|

所以x2+y2﹣3＝x2，

即x2＝4（x2+y2﹣3），

化简得，

∴点P的轨迹E的方程为：；

（2）设直线l的方程为：x＝my+1，P（x1，y1），Q（x2，y2），

联立方程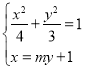，整理得：（4+3m2）y2+6my﹣9＝0，

∴，，

假设存在定点D（x0，0），使得x轴是∠PDQ的角平分线，则kPD+kQD＝0，

∴，

∴，

∴，

∴，

即，

解得：x0＝4，

所以存在定点D（4，0），使得x轴是∠PDQ的角平分线.