题目内容
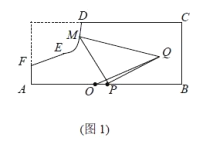
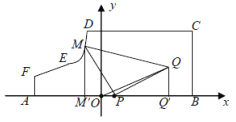
【题目】如图所示,某地区打算在一块矩形地块上修建一个牧场(ABCDEF围成的封闭区域)用来养殖牛和羊,其中AF=1,AB=10,BC=4,CD=7(单位:百米),DEF是一段曲线形马路.该牧场的核心区为等腰直角三角形MPQ所示区域,该区域用来养殖羊,其余区域养殖牛,且MP=PQ,牧场大门位于马路DEF上的M处,一个观察点P位于AB的中点处,为了能够更好观察动物的生活情况,现决定修建一条观察通道,起点位于距离观察点P处1百米的O点所示位置,终点位于Q处.如图2所示,建立平面直角坐标系,若![]() 满足
满足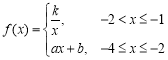 .
.
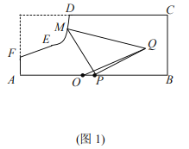
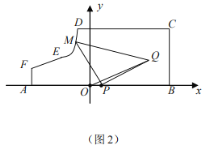
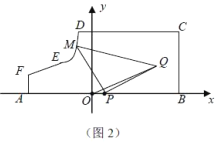
(1)求![]() 的解析式;
的解析式;
(2)求观察通道OQ长度的最小值.
【答案】(1)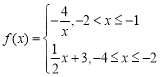 (2)
(2)![]() 百米
百米
【解析】
(1)依题意求出点![]() ,
,![]() ,
,![]() ,
,![]() 代入解析式即可求解;
代入解析式即可求解;
(2)过点M,Q分别作x轴的垂线,垂足为![]() ,
,![]() ,可得
,可得![]() ,
,
再对![]() 分类讨论,利用导数及二次函数的性质求出最小值;
分类讨论,利用导数及二次函数的性质求出最小值;
解:(1)因为AB=10,P是AB的中点,所以AP=5,
又OP=1,所以AO=4,所以![]() ,
,![]() ,
,
因为CD=7,BC=4,AF=1所以![]() ,
,![]()
由![]() 得,k=-4,所以
得,k=-4,所以![]() .
.
故![]() ,又
,又![]() ,所以
,所以![]() 解得
解得![]() ,
,
所以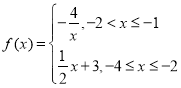
(2)过点M,Q分别作x轴的垂线,垂足为![]() ,
,![]() ,
,
则![]() ,
,
又因为PM⊥PQ,所以![]()
所以![]() ,又因为PM=PQ,所以
,又因为PM=PQ,所以![]() ,
,
所以,由![]() ,可得
,可得![]() ,
,
①若![]() ,设
,设![]() ,则
,则![]() ,
,
![]() .
.
令![]() ,则
,则![]()
![]() ,因为
,因为![]() ,所以
,所以![]()
所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]()
设![]() ,则
,则![]() 在
在![]() 上单调减
上单调减
所以![]() ,所以
,所以![]()
②若![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 时,
时,![]() ,
,
所以OQ的长度的最小值为![]() 百米.
百米.
答:观察通道OQ的长度的最小值为![]() 百米
百米

练习册系列答案
相关题目