题目内容
本小题 满分12分
满分12分
如图,在直三棱柱ABC—A1B1C1中,AC=1,AB=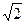 ,BC=
,BC=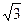 ,AA1=
,AA1=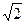 。
。
(I)求证:A1B⊥B1C;
(II)求二面角A1—B1C—B的大小。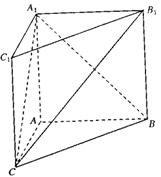
 满分12分
满分12分如图,在直三棱柱ABC—A1B1C1中,AC=1,AB=
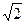 ,BC=
,BC=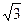 ,AA1=
,AA1=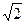 。
。(I)求证:A1B⊥B1C;
(II)求二面角A1—B1C—B的大小。

I)由AC=1,AB=
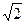 ,BC=
,BC=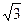 知AC2+AB2=BC2,
知AC2+AB2=BC2,所以AC⊥AB。
因为AB
 C—A1B1C1是直三棱柱,面ABB1A1⊥面ABC,
C—A1B1C1是直三棱柱,面ABB1A1⊥面ABC,所以AC⊥面ABB1A1。………………3分
由
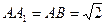 ,知侧面ABB1A1是正方形,连结AB1,
,知侧面ABB1A1是正方形,连结AB1,所以A1B⊥AB1
 。
。由三垂线定理得A1B⊥B1C。 ………………6分
(II)作BD⊥B1C,垂足为D,连结A1D。
由(I)知,A1B⊥B1C,则B1C⊥面A1BD,
于是B1C⊥A1D,
则∠A1DB为二面角
A1—B1C—B的平面角。………………8分
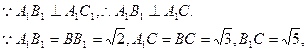
∴Rt△A1B1C≌Rt△B1BC,
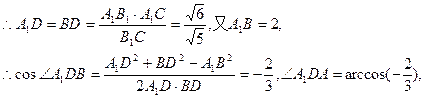
故二面角A1—B1C—B的大小为
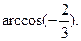 ………………12分
………………12分略

练习册系列答案
相关题目
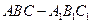 中,侧棱
中,侧棱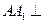 底面
底面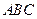 ,
,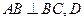 为
为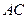 的中点,
的中点,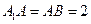 ,
,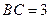 .
.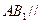 平面
平面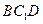 ;
;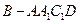 的体积.
的体积.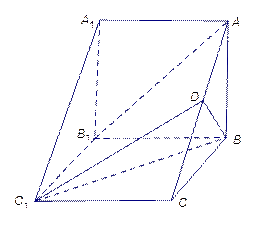 图5
图5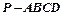 中,
中,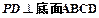 ,底面
,底面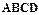 为正方形,
为正方形,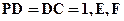 分别是
分别是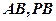 的中点.
的中点.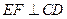 ;
;  求二面角
求二面角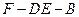 的大小;
的大小; 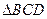 中,
中,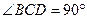 ,
,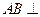 平面
平面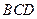 ,
,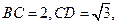
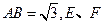 分别为
分别为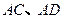 上的动点.
上的动点.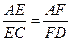 ,求证:平面
,求证:平面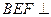 平面
平面 ;
;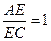 ,
,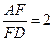 ,求平面
,求平面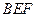 与平面
与平面
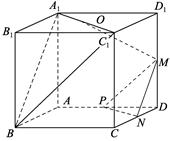
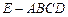 中,底面
中,底面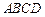 为矩形,平面
为矩形,平面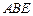 ,
,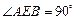 ,
,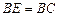 ,
,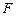 为
为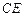 的中点,
的中点, 求证:
求证: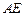 ∥平面
∥平面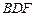 ;
;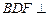 平面
平面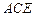 .
.
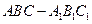 中,侧面
中,侧面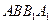 ,
,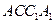 均为正方形,∠
均为正方形,∠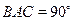 ,点
,点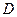 是棱
是棱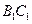 的中点.
的中点.
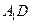 ⊥平面
⊥平面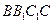 ;
;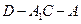 的余弦值.
的余弦值.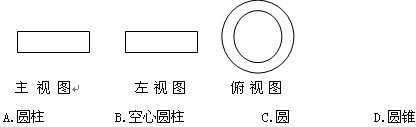
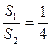 ,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则 ;
;