题目内容
(本题满分12分)
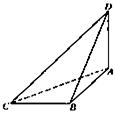
如图,在三棱柱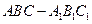 中,侧面
中,侧面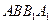 ,
,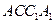 均为正方形,∠
均为正方形,∠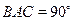 ,点
,点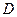 是棱
是棱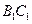 的中点.
的中点.
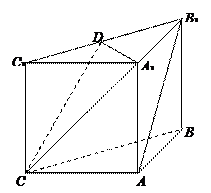
(Ⅰ)求证: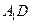 ⊥平面
⊥平面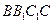 ;
;
(Ⅱ)求二面角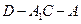 的余弦值.
的余弦值.
如图,在三棱柱
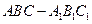 中,侧面
中,侧面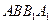 ,
,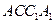 均为正方形,∠
均为正方形,∠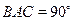 ,点
,点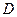 是棱
是棱 的中点.
的中点.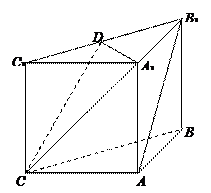
(Ⅰ)求证:
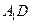 ⊥平面
⊥平面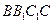 ;
;(Ⅱ)求二面角
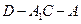 的余弦值.
的余弦值.(Ⅰ)证明:因为侧面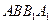 ,
,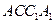 均为正方形,
均为正方形,

所以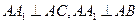 ,
,
所以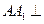 平面
平面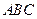 ,三棱柱
,三棱柱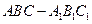 是直三棱柱. ………………1分
是直三棱柱. ………………1分
因为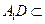 平面
平面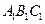 ,所以
,所以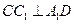 , ………………2分
, ………………2分
又因为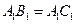 ,
,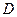 为
为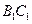 中点,∴
中点,∴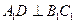 . ……………3分
. ……………3分
因为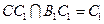 ,
,
所以 平面
平面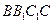 . ……………4分
. ……………4分
(Ⅱ)解: 因为侧面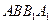 ,
,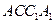 均为正方形,
均为正方形,
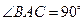 ,
,
所以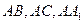 两两互相垂直,如图所示建立直角坐标系
两两互相垂直,如图所示建立直角坐标系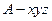 .
.
设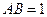 ,则
,则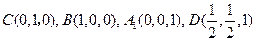
 .
.
 , ………………9分
, ………………9分
设平面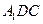 的法向量为
的法向量为 ,则有
,则有
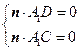 ,
,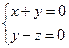 ,
, 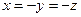 ,
,
取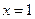 ,得
,得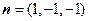 . ………………10分
. ………………10分
又因为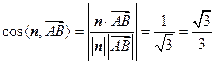
 平面
平面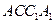 ,所以平面
,所以平面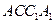 的法向量为
的法向量为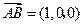 ,………11分因为二面角
,………11分因为二面角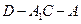 是钝角,
是钝角,
所以,二面角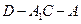 的余弦值为
的余弦值为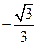 . ………………12分
. ………………12分
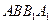 ,
,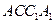 均为正方形,
均为正方形, 
所以
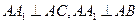 ,
,所以
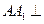 平面
平面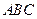 ,三棱柱
,三棱柱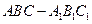 是直三棱柱. ………………1分
是直三棱柱. ………………1分因为
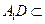 平面
平面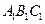 ,所以
,所以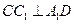 , ………………2分
, ………………2分又因为
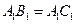 ,
,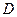 为
为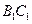 中点,∴
中点,∴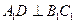 . ……………3分
. ……………3分因为
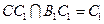 ,
,所以
 平面
平面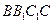 . ……………4分
. ……………4分(Ⅱ)解: 因为侧面
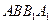 ,
,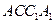 均为正方形,
均为正方形,
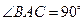 ,
,所以
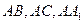 两两互相垂直,如图所示建立直角坐标系
两两互相垂直,如图所示建立直角坐标系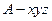 .
.设
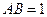 ,则
,则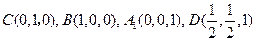
 .
. , ………………9分
, ………………9分设平面
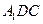 的法向量为
的法向量为 ,则有
,则有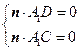 ,
,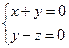 ,
, 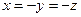 ,
,取
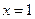 ,得
,得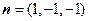 . ………………10分
. ………………10分又因为
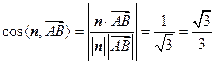
 平面
平面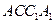 ,所以平面
,所以平面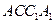 的法向量为
的法向量为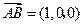 ,………11分因为二面角
,………11分因为二面角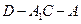 是钝角,
是钝角,所以,二面角
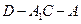 的余弦值为
的余弦值为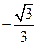 . ………………12分
. ………………12分略

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
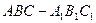 中,
中,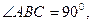
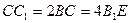
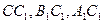 的中点,
的中点,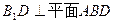 ;
;
 满分12分
满分12分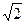 ,BC=
,BC=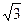 ,AA1=
,AA1=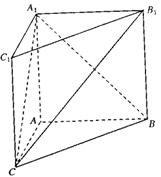
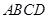 中,截面
中,截面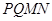 是正方形,则在下列命题中,错误的为( )
是正方形,则在下列命题中,错误的为( )
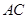 ∥截面
∥截面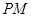 与
与 所成的角为
所成的角为
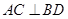
 ,BC=4,
,BC=4,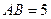 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.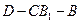 的余弦值.
的余弦值.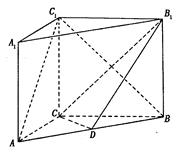
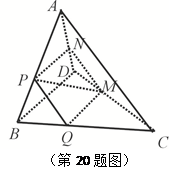
 的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC
的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC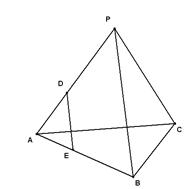
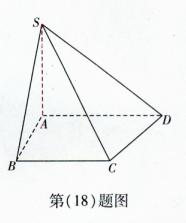
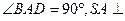 底面ABCD,SA=AB=BC=2,SD与平面ABCD所成角的正切值为
底面ABCD,SA=AB=BC=2,SD与平面ABCD所成角的正切值为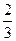 。
。
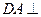 平面ABC,
平面ABC,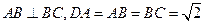 ,则球O的体积等于 。
,则球O的体积等于 。