题目内容
(本小题满分12分)
如图:在正方体ABCD—A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
(1) 求证:面MNP∥面A1C1B;(2) 求证:MO⊥面A1C1.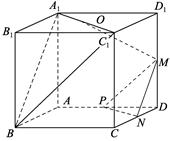
如图:在正方体ABCD—A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
(1) 求证:面MNP∥面A1C1B;(2) 求证:MO⊥面A1C1.

证明:(1) 连结D1C, MN为△DD1C的中位线,∴MN∥D1C.………………2分
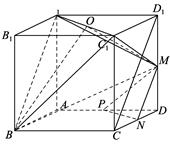
又∵D1C∥A1B∴MN∥A1B.同理MP∥C1B.…………………………………………… 4分
而MN与MP相交,MN,MP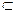 面MNP,A1B,
面MNP,A1B,
A1B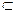 面A1C1B.∴面MNP∥面A1C1B.………………6分
面A1C1B.∴面MNP∥面A1C1B.………………6分
证明:(2) 法1,连结C1M和A1M,设正方体的边长为a,
∵正方体ABCD—A1B1C1D1,∴C1M=A1 M,
M,
又∵O为A1C1的中点,
∴A1C1⊥MO………………………………………………8分
连结BO和BM,在三角形BMO中,
经计算知:
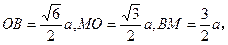 ∴OB2+MO2=MB2,
∴OB2+MO2=MB2,
即BO⊥MO.而A1C1,BO
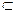 面A1C1B,∴MO⊥面A1C1B.
面A1C1B,∴MO⊥面A1C1B.
…………………………………………………………12分
法2,连结AB1,B1D,B1D1,则O是B1D1的中点,
∵AD⊥面ABB1A1,A1B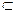 面ABB1A1,∴AD⊥A1B.
面ABB1A1,∴AD⊥A1B.
又A1B⊥A1B,AD和AB1是面AB1D内两条相交直线,
∴A1B⊥面AB1D,…………………………………………8分
又B1D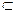 面AB1D,∴A1B⊥B
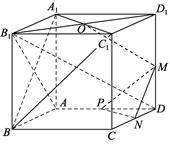
面AB1D,∴A1B⊥B 1D.同理:BC1⊥B1D. 第20题答案图(2)
1D.同理:BC1⊥B1D. 第20题答案图(2)
又A1B和BC1是面A1BC1内两条相交直线,∴B1D⊥面A1BC1.………………………10分
∵OM是△D1B1D的中位线,∴OM∥B1D.∴OM⊥面A1BC1.…………………………12分


又∵D1C∥A1B∴MN∥A1B.同理MP∥C1B.…………………………………………… 4分
而MN与MP相交,MN,MP
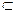 面MNP,A1B,
面MNP,A1B, A1B
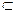 面A1C1B.∴面MNP∥面A1C1B.………………6分
面A1C1B.∴面MNP∥面A1C1B.………………6分
证明:(2) 法1,连结C1M和A1M,设正方体的边长为a,
∵正方体ABCD—A1B1C1D1,∴C1M=A1
 M,
M,又∵O为A1C1的中点,
∴A1C1⊥MO………………………………………………8分
连结BO和BM,在三角形BMO中,
|

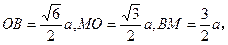 ∴OB2+MO2=MB2,
∴OB2+MO2=MB2,即BO⊥MO.而A1C1,BO

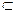 面A1C1B,∴MO⊥面A1C1B.
面A1C1B,∴MO⊥面A1C1B.…………………………………………………………12分
法2,连结AB1,B1D,B1D1,则O是B1D1的中点,
∵AD⊥面ABB1A1,A1B
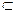 面ABB1A1,∴AD⊥A1B.
面ABB1A1,∴AD⊥A1B.又A1B⊥A1B,AD和AB1是面AB1D内两条相交直线,
∴A1B⊥面AB1D,…………………………………………8分
又B1D
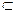 面AB1D,∴A1B⊥B
面AB1D,∴A1B⊥B 1D.同理:BC1⊥B1D. 第20题答案图(2)
1D.同理:BC1⊥B1D. 第20题答案图(2)又A1B和BC1是面A1BC1内两条相交直线,∴B1D⊥面A1BC1.………………………10分
∵OM是△D1B1D的中位线,∴OM∥B1D.∴OM⊥面A1BC1.…………………………12分
略

练习册系列答案
相关题目
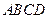 的上底
的上底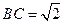 ,
,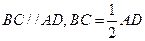 ,
,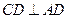 ,平面
,平面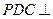 平面
平面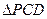 是边长为
是边长为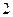 的等边三角形。
的等边三角形。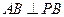 ;
;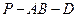 的大小。
的大小。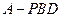 的体积。
的体积。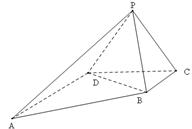
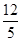
 满分12分
满分12分 ,BC=
,BC=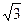 ,AA1=
,AA1=
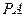 ⊥矩形
⊥矩形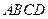 所在的平面,
所在的平面,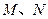 分别是
分别是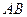 、
、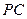 的中点,
的中点,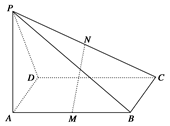
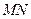 ∥平面
∥平面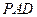 ;
;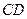 ;
;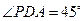 ,求证:平面
,求证:平面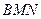 ⊥平面
⊥平面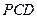 .
. ,BC=4,
,BC=4,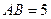 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.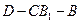 的余弦值.
的余弦值.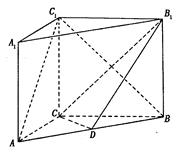


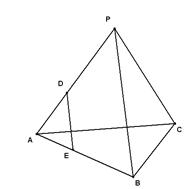
 的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC
的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC