题目内容
【题目】已知椭圆
：
的离心率为
，其左焦点与抛物线
的焦点重合.
（1）求椭圆的方程；
（2）过动点
的直线交
轴于点
，交椭圆于点
，
在第一象限，
，过点做轴的垂线交椭圆于点
，连接
并延长交椭圆于另一点
.设直线
的斜率分别为
，证明：
为定值.
【答案】（1）
（2）见证明
【解析】
（1）先由抛物线方程求得抛物线的焦点，可得c=1，再由椭圆的离心率可求得a，再由a，b，c的关系可以求出b，然后得到椭圆的方程.
（2）由直线过x轴上定点
，所以设出直线的横截式方程，先计算B点坐标，又因为
，所以根据线段的比例关系可以得到A的坐标，再由对称关系得到D点坐标，由两点式计算直线DT的斜率，然后求比值.
（1）由题意可知题意
的左焦点为
，因为离心率为
，
所以
，
所以题意的方程为.
（2）设直线
的方程为
，（
），则
，可求得
；
因为，
所以
，且
，
所以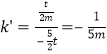
，
所以
为定值.
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】某蛋糕店制作并销售一款蛋糕，当天每售出
个利润为
元，未售出的每个亏损
元.根据以往
天的统计资料，得到如下需求量表，元旦这天，此蛋糕店制作了
个这种蛋糕.以
（单位：个， 
）表示这天的市场需求量. 
（单位：元）表示这天售出该蛋糕的利润.
需求量/个 |
|
|
|
|
|
天数 | 10 | 20 | 30 | 25 | 15 |
（1）将
表示为
的函数，根据上表，求利润
不少于
元的概率；
天的平均需求量（同一组数据用该区间的中点值作代表）；
（3）元旦这天，该店通过微信展示打分的方式随机抽取了
名市民进行问卷调查，调查结果如下表所示，已知在购买意愿强的市民中，女性的占比为
.
购买意愿强 | 购买意愿弱 | 合计 | |
女性 | 28 | ||
男性 | 22 | ||
合计 | 28 | 22 | 50 |
完善上表，并根据上表，判断是否有
的把握认为市民是否购买这种蛋糕与性别有关？
附： 
.
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
