题目内容
【题目】已知函数f (x)=ln x+x2-ax(a为常数).
(1)若x=1是函数f (x)的一个极值点,求a的值;
(2)当0<a≤2时,试判断f (x)的单调性;
(3)若对任意的a∈(1,2),x0∈[1,2],不等式f (x0)>mln a 恒成立,求实数m的取值范围.
【答案】(1)3;(2)见解析;(3)![]()
【解析】试题分析:(1)求出![]() ,由
,由![]() 列方程即可求
列方程即可求![]() 的值;(2)求出
的值;(2)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;;(3)问题等价于:对任意的
的减区间;;(3)问题等价于:对任意的![]() ,不等式
,不等式![]() 恒成立,即
恒成立,即![]() 恒成立,利用导数研究函数的单调性,根单调性求出
恒成立,利用导数研究函数的单调性,根单调性求出![]() 的最小值,进而可得结果.
的最小值,进而可得结果.
试题解析: f ′(x)=![]() +2x-a.
+2x-a.
(1)由已知得:f ′(1)=0,所以1+2-a=0,所以a=3,经验证符合题意.
(2)当0<a≤2时,f ′(x)=![]() +2x-a=
+2x-a=![]()
=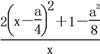 .
.
因为0<a≤2,所以1-![]() >0,而x>0,
>0,而x>0,
即f ′(x)=![]() >0,
>0,
故f (x)在(0,+∞)上是增函数.
(3)当a∈(1,2)时,由(2)知,f (x)在[1,2]上的最小值为f (1)=1-a,
故问题等价于:对任意的a∈(1,2),
不等式1-a>mln a恒成立,即m<![]() 恒成立.
恒成立.
记g(a)=![]() (1<a<2),则g′(a)=
(1<a<2),则g′(a)=![]() .
.
令M(a)=-aln a-1+a,则M′(a)=-ln a<0,
所以M(a)在(1,2)上单调递减,
所以M(a)<M(1)=0,故g′(a)<0,
所以g(a)=![]() 在a∈(1,2)上单调递减,
在a∈(1,2)上单调递减,
所以m≤g(2)=![]() =-log2e,
=-log2e,
即实数m的取值范围为(-∞,-log2e].

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目