题目内容
【题目】如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).

(1)若M为PC的中点,求证:PA∥平面BME;
(2)是否存在点M,使二面角MBED的大小为30°.若存在,求出点M的位置;若不存在,说明理由.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)连接AC交BE于点F,根据平几知识可得ABCE为平行四边形,即得MF∥PA. 再根据线面平行判定定理得结论(2)先根据空间直角坐标系,再设立各点坐标,根据方程组解得平面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补关系列方程解得M坐标,即得点M的位置.
试题解析:(1)证明:如图,连接AC交BE于点F,连接CE.
由题意知BC∥AE,且BC=AE,故四边形ABCE为平行四边形,∴F为AC的中点,在△PAC中,又由M为PC的中点,得MF∥PA.
又MF平面BME,PA平面BME,∴PA∥平面BME.
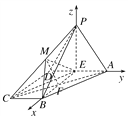
(2)连接PE,则由题意知PE⊥平面ABCD.
故以E为坐标原点建立如图所示空间直角坐标系E-xyz,则
E(0,0,0),P(0,0,![]() ),
),
B(![]() ,0,0),C(
,0,0),C(![]() ,-1,0).
,-1,0).
设![]() =λ
=λ![]() =(0<λ<1),
=(0<λ<1),
则M(![]() λ,-λ,
λ,-λ,![]() (1-λ)).
(1-λ)).
∴![]() =(
=(![]() λ,-λ,
λ,-λ,![]() (1-λ)),
(1-λ)),![]() =(
=(![]() ,0,0).
,0,0).
取平面DBE的法向量n1=(0,0,1),设平面BME的法向量n2=(x,y,z),
则由
得![]() 令y=
令y=![]() ,得n2=
,得n2=![]() .
.
又由![]() =cos30°,得λ=
=cos30°,得λ=![]() ,
,
即M![]() .故存在点M满足要求,且M为棱PC上靠近端点C的四等分点.
.故存在点M满足要求,且M为棱PC上靠近端点C的四等分点.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】某教育培训中心共有25名教师,他们全部在校外住宿.为完全起见,学校派专车接送教师们上下班.这个接送任务承包给了司机王师傅,正常情况下王师傅用34座的大客车接送教师.由于每次乘车人数不尽相同,为了解教师们的乘车情况,王师傅连续记录了100次的乘车人数,统计结果如下:
乘车人数 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
频数 | 2 | 4 | 4 | 10 | 16 | 20 | 16 | 12 | 8 | 6 | 2 |
以这100次记录的各乘车人数的频率作为各乘车人数的概率.
(Ⅰ)若随机抽查两次教师们的乘车情况,求这两次中至少有一次乘车人数超过18的概率;
(Ⅱ)有一次,王师傅的大客车出现了故障,于是王师傅准备租一辆小客车来临时送一次需要乘车的教师.可供选择的小客车只有20座的![]() 型车和22座的
型车和22座的![]() 型车两种,
型车两种, ![]() 型车一次租金为80元,
型车一次租金为80元, ![]() 型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?
型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?



