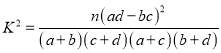题目内容
【题目】已知函数![]() .
.
(1)判断并证明![]() 的奇偶性;
的奇偶性;
(2)用单调性的定义证明函数![]() 在其定义域上是增函数;
在其定义域上是增函数;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)f(x)是奇函数,证明见解析(2)证明见解析(3)(﹣∞,![]() )
)
【解析】
(1)利用函数奇偶性的定义即可判断与证明;
(2)按照单调性定义证明的步骤,取值-作差-变形-定号-下结论,即可证出;
(3)利用函数的奇偶性和单调性,将抽象不等式![]() 可转化为
可转化为
![]() ,解出即可.
,解出即可.
(1)因为定义域为![]() ,
,
f(﹣x)=1![]() 1﹣2
1﹣2![]() 1
1![]()
1﹣2![]() (1
(1![]() )=﹣f(x),
)=﹣f(x),
所以f(x)是奇函数;
(2)证明:设x2>x1,则f(x2)﹣f(x1)=(1![]() )﹣(1
)﹣(1![]() )
)
=2 ,
,
由题设可得:3![]() 3
3![]() 0,(1+3
0,(1+3![]() )>0,(1+3
)>0,(1+3![]() )>0,
)>0,
∴2 0,
0,
即f(x2)﹣f(x1)>0,故f(x)在其定义域上是增函数;
(3)不等式f(3m+1)+f(2m﹣3)<0,f(3m+1)<﹣f(2m﹣3)=f(3﹣2m),
∴3m+1<3﹣2m,解得m![]() ,即不等式的解集为(﹣∞,
,即不等式的解集为(﹣∞,![]() ).
).

【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”