题目内容
【题目】在平面直角坐标系xoy中,点 ![]() ,圆F2:x2+y2﹣2
,圆F2:x2+y2﹣2 ![]() x﹣13=0,以动点P为圆心的圆经过点F1 , 且圆P与圆F2内切.
x﹣13=0,以动点P为圆心的圆经过点F1 , 且圆P与圆F2内切.
(1)求动点的轨迹的方程;
(2)若直线l过点(1,0),且与曲线E交于A,B两点,则在x轴上是否存在一点D(t,0)(t≠0),使得x轴平分∠ADB?若存在,求出t的值;若不存在,请说明理由.
【答案】
(1)解:圆F2:x2+y2﹣2 ![]() x﹣13=0化为
x﹣13=0化为 ![]() .
.
故F2( ![]() ),半径r=4.
),半径r=4.
而 ![]() <4,∴点F1在圆F2内,
<4,∴点F1在圆F2内,
又由已知得圆P的半径R=|PF1|,由圆P与圆F2内切得,圆P内切于圆F2,即|PF2|=4﹣|PF1|,
∴|PF1|+|PF2|=4>|F1F2|,
故点P的轨迹是以F1、F2为焦点,长轴长为4的椭圆,
有c= ![]() ,a=2,则b2=a2﹣c2=1.
,a=2,则b2=a2﹣c2=1.
故动点的轨迹方程为 ![]()
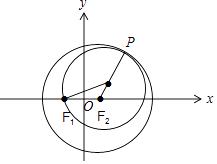
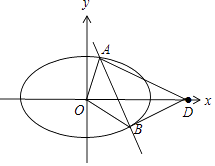
(2)解:设A(x1,y1),B(x2,y2),
当直线l的斜率不为0时,设直线l:x=ny+1.
联立 ![]() ,得(n2+4)y2+2ny﹣3=0.
,得(n2+4)y2+2ny﹣3=0.
△=16(n2+3)>0恒成立.
![]() ,
, ![]() .①
.①
设直线DA、DB的斜率分别为k1,k2,则由∠ODA=∠ODB得,
![]() =
= ![]()
= ![]() =
= ![]() .
.
∴2ny1y2+(1﹣t)(y1+y2)=0,②
联立①②,得n(t﹣4)=0.
故存在t=4满足题意;
当直线l的斜率为0时,直线为x轴,取A(﹣2,0),B(2,0),满足∠ODA=∠ODB.
综上,在x轴上存在一点D(4,0),使得x轴平分∠ADB.
【解析】(1)化圆的方程为标准方程,求出圆心坐标和半径,画出图形,数形结合可得|PF1|+|PF2|=4>|F1F2|,故点P的轨迹是以F1、F2为焦点,长轴长为4的椭圆, 由此求出动点的轨迹方程;(2)设A(x1 , y1),B(x2 , y2),当直线l的斜率不为0时,设直线l:x=ny+1.联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求得A,B的纵坐标的和与积,结合斜率关系求得t值;当直线l的斜率为0时,直线为x轴,取A(﹣2,0),B(2,0),满足∠ODA=∠ODB.综上,在x轴上存在一点D(4,0),使得x轴平分∠ADB.

 阅读快车系列答案
阅读快车系列答案