题目内容
【题目】已知在梯形ABCD中,∠ADC= ![]() ,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE.
,AB∥CD,PC⊥平面ABCD,CP=AB=2DC=2DA,点E在BP上,且EB=2PE. 
(1)求证:DP∥平面ACE;
(2)求二面角E﹣AC﹣P的余弦值.
【答案】
(1)证明:连接DB交AC于点O,连接OE,
∵AB∥CD,∴ ![]() ,
,
∵EB=2PE,∴ ![]() ,
,
∴OE∥PD.
∵DP平面ACE,OE平面ACE,
∴DP∥平面ACE
(2)解:设CD=1,∵∠ADC= ![]() ,且PC⊥平面ABCD,
,且PC⊥平面ABCD,
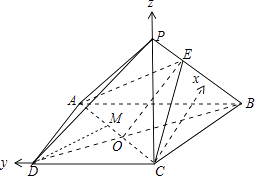
故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.
则C(0,0,0),A(1,1,0),B(1,﹣1,0),D(0,1,0),P(0,0,2),
设E(xE,yE,zE),由EB=2PE,得 ![]() ,
,
∴(xE,yE,zE﹣2)= ![]() (1,﹣1,﹣2),得E(
(1,﹣1,﹣2),得E( ![]() ).
).
![]() ,
,
设平面ACE的一个法向量为 ![]() .
.
由 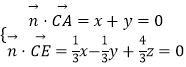 ,取x=1,得
,取x=1,得 ![]() .
.
取AC的中点M,连接MD,可得M( ![]() ),
),
∴ ![]() .
.
由DA=DC,得MD⊥AC,
由PC⊥底面ABCD,得MD⊥PC,
又AC∩PC=C,∴MD⊥平面PAC,
∴ ![]() 是平面PAC的一个法向量.
是平面PAC的一个法向量.
∴|cos< ![]() >|=
>|=  .
.
由图可知,二面角E﹣AC﹣P为锐二面角,
∴二面角E﹣AC﹣P的余弦值为 ![]() .
.
【解析】(1)连接DB交AC于点O,连接OE,由已知结合平行线成比例可得OE∥PD.再由线面平行的判定可得DP∥平面ACE;(2)设CD=1,由∠ADC= ![]() ,且PC⊥平面ABCD,故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.求出平面ACE的一个法向量,再证明MD⊥平面PAC,可得
,且PC⊥平面ABCD,故以C为原点,过点C与AD平行的直线为x轴,CD所在直线为y轴,CP所在直线为z轴距离空间直角坐标系.求出平面ACE的一个法向量,再证明MD⊥平面PAC,可得 ![]() 是平面PAC的一个法向量.由两法向量所成角的余弦值求得二面角E﹣AC﹣P的余弦值.
是平面PAC的一个法向量.由两法向量所成角的余弦值求得二面角E﹣AC﹣P的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系,随机调查了该社区5户家庭,得到如下统计数据表:
购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
根据上表可得回归直线方程 ![]() ,其中
,其中 ![]() ,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
A.1.79万元
B.2.55万元
C.1.91万元
D.1.94万元
